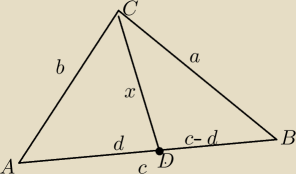
Wykaż Krzysiek: Niech x oznacza długość dowolnego odcinka którego jednym końcem jest wierzchołek trójkąta a drugim punkt leżący na boku naprzeciw tego wierzchołka . Mamy udowodnic że x>(a+b−c)/2 x≤b+d x≤a+(c−d) 2x≤a+b+c x≤(a+b+c)/2 Mamy inna nierownośc udowodnić x+d≥b x+c−d≥a 2x+c≥a+b 2x≥a+b−c x≥(a+b−c)/2 We wskazówce do zadania jest napisane żeby zwrócić uwagę na to że równość zachodzi co najwyżej raz . raz Czyli albo wcale albo raz. Kiedy zachodzi raz?

Krzysiek:

Tadeusz: ... z którym masz problem?

Krzysiek: Z nierówności trójkąta ogólnie jesli mamy 3 punkty A B C ||AB|−|BC||≤|AC|≤|AB|+|BC| W zadaniu jest napisane że to wierzchołek trójkąta więc te punkty nie mogą być współliniowe więc od razu można było pisać (>) W odpowiedzi daje nieróność (≥) a potem każe sie zastanawiać dlaczego równośc zachodzi tylko raz więc należy dac nierównośc (>)