rachunek prawdopodobieństwa jendrzej: Mam zadanie W kartonie znajduje się 20 żarówek, w tym pewna liczba żarówek wadliwych. Wybieramy kolejno bez zwracania dwie żarówki. Oblicz, ile co najwyżej dobrych żarówek znajduje się w tym kartonie, jeżeli prawdopodobieństwo wylosowania za drugim razem dobrej żarówki jest większy od 0,1

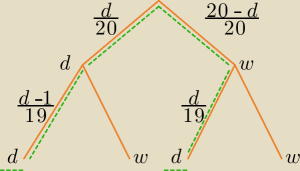
ite: d − ilość dobrych żarówek 20−d − ilość wadliwych Zsumuj prawdopodobieństwa z zielonych "ścieżek" prowadzących do wylosowania za drugim razem dobrej żarówki. Wynik ma być większy od 0,1. I taką nierówność rozwiąż.

wredulus_pospolitus: Chcemy wylosować dobrą żarówkę za drugim razem.

	d		2		1
P(Dobra2) = P(Dobra1) =		>		=		= 0.1
	20		20		10

dobrych żarówek mamy co najmniej 2 sztuki Do autora: Warto zapamiętać −−−− jeżeli zdarzenie polega na losowaniu czegoś (bez zwracania) z danej puli to prawdopodobieństwo sukcesu (czy też porażki) w każdej rundzie losowania będzie jednakowe i równe prawdopodobieństwo sukcesu (czy też porażki) w pierwszym losowaniu −−−− tak długo jak długo nie mamy informacji co zostało wylosowane w poprzednich rundach. Popatrz na to w ten sposób: Masz 5 kart (10,Walet, Dama, Król, As) i pięciu kolegów wyciąga kolejno kartę, jaką szansę ma każdy z nich na wyciągnięcie Asa? Przed przystąpieniem do losowania każdy z nich będzie miał prawdopodobieństwo równe 1/5 − prawda ?! Więc w trakcie (jeżeli nie wiemy co inni wylosowali) także będzie to równe 1/5.