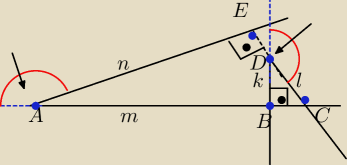
Dowód Mu Zhuohua: Mam udowodnic twierdzenie że jeśli mam dwa kąty które maja ramiona odpowiednio prostopadłe to te kąty są równe jeśli oba są albo ostre albo rozwarte Dowód zrobiony dla kątów ostrych że kąt A = kątowi D Biorąc pod uwage Δ prostokątne AEC i BDC kąt A= 90^o−C i kąt D=90^o−C stąd kąt A= kątowi D Moje pytanie jest takie Czy należy wobec tego jeszcze robić dowód dla kątów rozwartych (tzn przyległych do kątów A i B ) czy wtedy wystarczy napisać −skoro kąty A i D są rowne to kąty przyległe do A tez są rowne i ich miara wynosi 180^o−A? czy osobno należy przeprowadzic dowód −jesli tak to jak by to miało wyglądac bo nie widze jakie wtedy trójkaty prostokątne brać pod uwagę . dziękuje

ite: 👉 wstawienie treści zadania pomoże zrozumieć problem

ite: "Dowód zrobiony dla kątów ostrych że kąt A = kątowi D" → czyli nie dla tych z rysunku (ich miar)?

Mu Zhuohua: Dzień dobry ite Treśc zadania jest dokładnie taka jak napisałem (czyli udowodnic to twierdzenie . Strzałkami oznaczyłem kąty przyległe do A i D z lenistwa . fakt jest to niechlujnie

. : Łatwiej byłoby zauważyć podobieństwo trójkątów ABC i DE'brak oznaczenia' Wtedy mamy dwa takie same katy które są dopełnieniem do 180^o kątów o których mowa w zadaniu