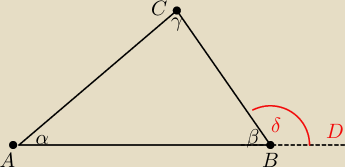
Dowód -kąt zewnętrzny Mu Zhuohua: Takie dwa dowody trochę dla mnie ciężkie Pierwszy to Wykazać że kąt zewnętrzny trójkąta jest większy od każdego kąta wewnętrznego nieprzyległego do kąta zewnętrznego ∡CBD=δ − kąt zewnętrzny ∡δ>∡α i ∡δ>∡γ

Mu Zhuohua: Drugi dowód miał byc inny ale wpisze go na nowe zadanie natomiast skoro już jestem przy kątach zewnętrznych trójkąta to Wykazać ze miara kąta zewnętrznego trójkąta jest równa sumie miar kątów wewnętrznych do niego nieprzyległych Mamy wykazać że δ=α+γ−nasza teza α+β+γ=180^o β=180^o−(α+γ) δ=180^o−β δ=180^o−(180^o−(α+γ)) δ=α+γ ckd Do tego dowodu trzeba jeszcze pokazać dla kąta α i kąta γ? Zrobiłem tylko dla kąta β

Guabuła: δ= α+γ > α δ= α+γ > γ

Mu Zhuohua: Dobrze. I to wystarczy? Bo w książce najpierw miałem o tym że ten kąt jest większy od każdego pozostałego a dopiero potem o równości tych kątów

wredulus_pospolitus: 1. α + γ = 180^o − β = δ −−−> δ > α ∧ δ > γ

wredulus_pospolitus: jeszcze można było dopisać: α,β,γ,δ > 0^o

Mu Zhuohua: Ogólnie nie cierpię tych dowodów ale chcieli w zadaniu Mam tak w książce ale pomyślałem że można będzie nie tak aż bardzo cierpieć https://zapodaj.net/plik-5wZb4HWBMZ

Mu Zhuohua: Wrzucę jeszcze dalszą część może ktoś tez skorzysta https://zapodaj.net/plik-EzxS9uO7AZ