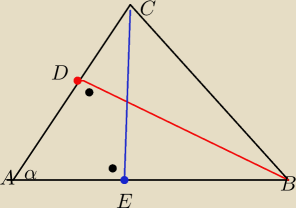
Dowód KlasaV-VIII-: W trójkącie ABC wysokość BD względem boku AC i wysokość CE względem boku AB są równe Udowodnić ze trójkąt ABC jest równoramienny Założenie dany trójkąt ABC i BD=CE Teza: Trójkąt ABC jest równoramienny Dowód : Z założenia EC=BD Kąty ADB i AEC maja miare po 90^o Kat α jest wspólny dla obu trójkątów Stąd ΔAEC≡ ΔADB Z przystawania tego wynika że AE=AD i AC=AB gdyż są to przeciwprostokątne tych trójkątów Stąd wynika ze trójkąt ABC jest równoramienny

wredulus_pospolitus: Alternatywne podejście:

|AC|*|BD|		|AB|*|CE|
	= PΔAB =
2		2

skoro |BD| = |CE| to

|AC|*|BD|		|AB|*|CE|
	= PΔAB =
2		2

|AC|*|BD| − |AB|*|CE| = 0 |BD|*(|AC| − |AB|) = 0 −−−> |AC| = |AB|

KlasaV-VIII-: Witam i dziękuje Przerabiam teraz sobie przystawanie trójkątów i bedę miał trochę zadań z tego Następna lekcja to dwie proste przecięte sieczną i związane z tym kąty