Środkowa w trójkącie
KlasaV-VIII:
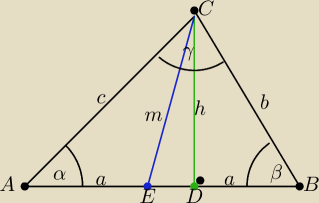
Mamy trójkąt ABC
|CD=h wysokość trójkąta
|CE|=m
c środkowa trójkata poprowadzona z punktu C na bok AB
|AE|=|EB|=a
|BC|=b
|AC|=c
Środkowa dzieli nam trójkąt ABC na dwa trójkąty o równych polach.
P
ΔAEC=P
ΔEBC
h− wspólna wysokość dla obu trójkątów
Możemy więc zapisać że
P
ΔAEC= 0,5a*h
P
ΔEBC= 0,5a*h
stąd P
ΔAEC=P
ΔEBC
Mozemy też zapisać że
P
ΔAEC= 0,5a*c*sinα
P
ΔEBC= 0,5a*b*sinβ
Jak to wykazac że te pola są równe?
27 wrz 23:56
KlasaV-VIII:
Dobrze już widzę
Nie te boki wziąlem
∡|AEC|=β to ∡|CEB=180o−β
PΔAEC= 0.5*a*m*sinβ
PΔCEB= 0,5a*m*sin(180o−β)= 0,5a*m*sinβ
Stąd PΔAEC=PΔCEB
28 wrz 00:13
Antek: Mylący jest Twój nick. Zapewne tylko dla mnie, a może nie? Bo dzielisz się rozwiązaniami
ciekawych zadań, niektóre z nich konsultujesz, ale wiele z nich wybiega poza poziom klas
V−VIII.
Jasne, że nic mi do tego, więc mnie nie ochrzaniaj, tylko podumaj nad tym. Pozdrawiam

28 wrz 00:26
KlasaV-VIII:
Również pozdrawiam

Ja niedawno napisałem że wracam do podstawówki
Tak naprawdę to ze mną jest inny problem ale to nie miejsce i czas żeby o tym pisać.
Nick mogę oczywiście zmienić np na emeryt

28 wrz 00:42
Antek: Tak, Emeryt to byłby strzał w 10−tkę, ale inny także

Swoją drogą podziwiam Twoją pasję do matematyki, to ogromne zaangażowanie, które widać gołym
okiem.
Ale że tu wchodzi sporo uczniów, to apriori oni ominą Twoje ciekawe zadania, np. maturzyści, a
wielka szkoda, bo mogą się od Ciebie sporo nauczyć.
Pozdrawiam serdecznie

28 wrz 00:46
KlasaV-VIII:
Teraz akuratnie powtarzam geometrię więc pewnie będę dużo dopytywał
Od stycznia już jestem na emeryturze

28 wrz 00:50
Antek: 
Dobrej nocy życzę.
28 wrz 00:55
KlasaV-VIII:
Dobranoc

28 wrz 00:58
28 wrz 01:04
 Mamy trójkąt ABC
|CD=h wysokość trójkąta
|CE|=mc środkowa trójkata poprowadzona z punktu C na bok AB
|AE|=|EB|=a
|BC|=b
|AC|=c
Środkowa dzieli nam trójkąt ABC na dwa trójkąty o równych polach.
PΔAEC=PΔEBC
h− wspólna wysokość dla obu trójkątów
Możemy więc zapisać że
PΔAEC= 0,5a*h
PΔEBC= 0,5a*h
stąd PΔAEC=PΔEBC
Mozemy też zapisać że
PΔAEC= 0,5a*c*sinα
PΔEBC= 0,5a*b*sinβ
Jak to wykazac że te pola są równe?
Mamy trójkąt ABC
|CD=h wysokość trójkąta
|CE|=mc środkowa trójkata poprowadzona z punktu C na bok AB
|AE|=|EB|=a
|BC|=b
|AC|=c
Środkowa dzieli nam trójkąt ABC na dwa trójkąty o równych polach.
PΔAEC=PΔEBC
h− wspólna wysokość dla obu trójkątów
Możemy więc zapisać że
PΔAEC= 0,5a*h
PΔEBC= 0,5a*h
stąd PΔAEC=PΔEBC
Mozemy też zapisać że
PΔAEC= 0,5a*c*sinα
PΔEBC= 0,5a*b*sinβ
Jak to wykazac że te pola są równe?

 Ja niedawno napisałem że wracam do podstawówki
Tak naprawdę to ze mną jest inny problem ale to nie miejsce i czas żeby o tym pisać.
Nick mogę oczywiście zmienić np na emeryt
Ja niedawno napisałem że wracam do podstawówki
Tak naprawdę to ze mną jest inny problem ale to nie miejsce i czas żeby o tym pisać.
Nick mogę oczywiście zmienić np na emeryt 
 Swoją drogą podziwiam Twoją pasję do matematyki, to ogromne zaangażowanie, które widać gołym
okiem.
Ale że tu wchodzi sporo uczniów, to apriori oni ominą Twoje ciekawe zadania, np. maturzyści, a
wielka szkoda, bo mogą się od Ciebie sporo nauczyć.
Pozdrawiam serdecznie
Swoją drogą podziwiam Twoją pasję do matematyki, to ogromne zaangażowanie, które widać gołym
okiem.
Ale że tu wchodzi sporo uczniów, to apriori oni ominą Twoje ciekawe zadania, np. maturzyści, a
wielka szkoda, bo mogą się od Ciebie sporo nauczyć.
Pozdrawiam serdecznie 

 Dobrej nocy życzę.
Dobrej nocy życzę.



