 Boki trójkąta ABC mają długość |AB| = 8 |BC| = 11 |CD| = 5. Odcinek CD jest środkową w tym
trójkącie, a odcinek BE jest środkową w trójkącie BCD. Oblicz długość odcinka BE.
Rozrysowałem sobie wszystko w taki sposób i trochę utknąłem. Z jakich zależności należy tu
skorzystać?
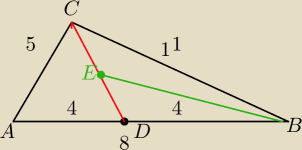
Boki trójkąta ABC mają długość |AB| = 8 |BC| = 11 |CD| = 5. Odcinek CD jest środkową w tym
trójkącie, a odcinek BE jest środkową w trójkącie BCD. Oblicz długość odcinka BE.
Rozrysowałem sobie wszystko w taki sposób i trochę utknąłem. Z jakich zależności należy tu
skorzystać?
 |CD|=0,5√2(|AC|2+|BC|2)−|AB|2
|CD|= 0,5*√2(25+121)−64
|CD|=0,5√2(|AC|2+|BC|2)−|AB|2
|CD|= 0,5*√2(25+121)−64
| 1 | 1 | 1 | ||||
|CD|=0,5*√2*146−64=0,5*√292−64= | *√228= | *√4*57= | * 2√57=√57 | |||
| 2 | 2 | 2 |
| 1 | ||
|BE|= | √2(16+121−57= licz dalej | |
| 2 |
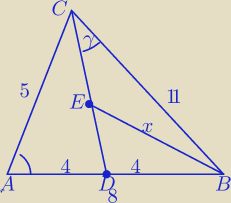 CD możesz obliczyć z tw. cosinusów
1) Tw. cosinusów
ΔABC:
112=82+52−2*8*5cos(A)
CD możesz obliczyć z tw. cosinusów
1) Tw. cosinusów
ΔABC:
112=82+52−2*8*5cos(A)
| 2 | ||
cos(A)=− | ||
| 5 |
| 2 | ||
CD2=42+52−2*4*5*(− | ) | |
| 5 |
| √217 | ||
x= | ||
| 2 |
| 1 | ||
|BE|= | √2(|DB|2+|BC|2)−|CD|2 | |
| 2 |
 Potem dla siebie spróbuje to zrobić inaczej z twierdzenia cosinusów
Potem dla siebie spróbuje to zrobić inaczej z twierdzenia cosinusów
| √217 | ||
|BE|= | ||
| 2 |
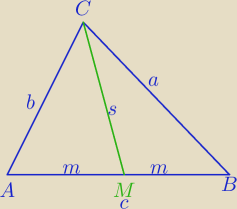 Możesz jeszcze łatwiej rozwiązać problem.
Twierdzenie Apoloniusza.
CM− środkowa
AC2+BC2=2 CM2+2*AM2
albo tak zapisać:
a2+b2=2s2+2*m2
Możesz jeszcze łatwiej rozwiązać problem.
Twierdzenie Apoloniusza.
CM− środkowa
AC2+BC2=2 CM2+2*AM2
albo tak zapisać:
a2+b2=2s2+2*m2
 Na razie wracam do podstawówki
Na razie wracam do podstawówki