zadanie z trygonometrii buba:

	√5
suma cosinusów kątów ostrych w pewnym trójkącie prostokątnym wynosi		. Oblicz sumę
	2

kwadratów tangensów tych kątów.

Monika: Jeśli narysujesz sobie trójkąt prostok. o przyprost. a i b oraz przeciwprostok. c, to zauważysz, że cos alfa to b/c zaś cos beta to a/c czyli sin alfa. Zatem cos alfa + sin alfa = pierw. z 5 przez 2. Podnieś obustronnie do kwadratu, zastosuj wzór na kwadrat sumy.

Monika: A może tak, z innego wzoru, jeśli go masz w programie nauczania: cosα+cosβ= 2cos(α+β) /2 razy cos(α−β) /2 i wtedy √5 /2 = 2 cos 45 stopni razy cos (α−β) /2

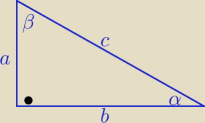
baba jaga: W trójkacie prostokątnym: cosβ=sinα i tgβ= ctgα to cosα+cosβ= cosα+sinα i tg²α+tg²β= tg²α+ctg²β

	√5
cosα+sinα=		|2
	2

1+2sinαcosα= 5/4 ⇒ sinαcosα= 1/8

	cos2α+sin2α
tg2α+ctg2α= (tgα+ctgα)2−2tgα*ctgα= (		)2−2 ( bo tgα*ctgα=1
	sinαcosα

	1		1
= (		)2−2=(		)2−2 = 64−2=62
	sinαcosα		1   8

buba: Bardzo wszystkim dziękuję za pomoc.