planimetria ~~miks: W trójkacie ABC poprowadzono odcinki AD, BE i CF w ten sposób, z˙ e punkty D, E i F sa˛ srodkami odpowiednio odcinków BE, CF i AD. Oblicz pole trójkata ABC jezeli pole trójkata DEF jest równe 2. Jak to rozwiazac wzorem P=0,5absinα. Wiem jaki jest wynik bo rozwiazanem wspólnymi wysokościami i podstawa, ale można tez tym wzorem jak ?

Mila: https://zadania.info/d289/3934640

~~miks: Dzięki, tak to ja mam rozwiązane, ale chcę tylko przy użyciu tego wzoru z sinusem

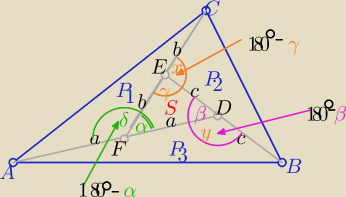
maks: S=2 2S= a*b*sinα = C*b*sinγ= a*c*sinγ= 4 sin(180^o−α)= sinα

	a*2b*sinδ
to P1=		= absinα= 4
	2

	b*2c*sinx
P2=		= bc sinγ= 4
	2

	c*2a*siny
P3=		= acsinβ =4
	2

P(ABC)= 3*4+2= 14

~~miks: Właśnie to,dzieki