proszę o rozwiązanie anna: w trójkącie równoramiennym ABC: AB jest podstawą, C(−2; 1) Prosta y = 2x − 5 jest symetralną AC jedna z wysokości trójkąta zawiera się w prostej y = x + 3 Wyznacz współrzędne wierzchołków A i B

wredulus_pospolitus: A co byłaś w stanie sama zrobić ?

anna: C ∊ y = x + 3 czyli należy do wysokości wspólny punkt przecięcia się wysokości i symetralnej K( 8 ;11) dalej nie wiem

chichi: symetralna AC, da Ci współczynnik kierunkowy prostej, w której zawarty jest bok AC, punkt C masz więc masz równanie tej prostej, rozwiązując układ składający się z równań tych prostych otrzymasz współrzędne punktu będące środkiem odcinka AC, więc łatwo ze wzoru na środek odcinka otrzymasz współrzędne punktu A. stąd jesteś w stanie otrzymać równanie prostej AB (prostopadła do prostej w której zawarta jest wysokość i przechodząca przez punkt A). Rozwiązując układ składający się z tych prostych otrzymasz środek AB i znów wzór na środek odcinka

anna: rozwiązałam zadanie według wskazówek chichi 15 wrz 2023 08:08 wyniki to A(6 ;−3) i B( −6 ; 9) proszę o sprawdzenie dziękuję bardzo

chichi: jest ok

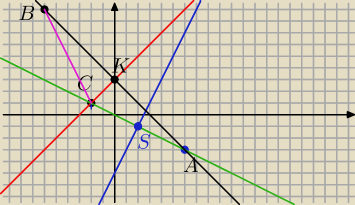
Klasa V-VIII: Współczynnik kierunkowy prostej AC m₁= −0,5x Rownanie prostej AC i przechodzącej przez punkt C (−2,1) y−1= −0,5(x+2) y=−0,5x (zielona Wspólrzedne S srodka odcinka AC {y=−0,5x {y=2x−5(niebieska x_s=2 y_s=−1 x_A= 2x_s−x_C x_A= 4−(−2)=6 y_A= 2y_S−y_c y_A= −2−1=−3 Punkt A(6,−3) y=x+3 (czerwona Wspólczynnik kieriunkowy prostej AB prostopadłej do y=x+3 m₂= −1 Równanie prostej AB i przechodzącej przez punkt A(6,−3) y+3= −1(x−6) y=−x+3(czarna Wspólrzedne punktu K srodka odcinka AB (y=x+3 [y=−x+3 x+3=−x+3 2x=0 x=0 y=3 Punkt K(0,3) 2x_K= x_A+x_B x_B= 2x_K−x_A x_B= 0−6=−6 2y_K= y_A+y_B y_B= 2y_K−y_A y_B= 6−(−3)= 9 Punkt B(−6,9) Powinno być dobrze. Ale sprawdz czy |AC|=|BC|

anna: dziękuję bardzo rysunek mam taki sam