Podzbiory zbioru Klasa 6 : Ile różnych podzbiorów można utworzyć ze zbioru a) A={a,b,c,d} b) B={a,b,c d,e} dla a) {abcd} {∅} {a} {b} {c} {d} {a,b} {ac}{ad} {bc} {bd} {cd} {abc} { acd} {bcd} Do b) {abcde} {∅} {a} {b} {c} {d} {e} {ab} {ac} {ad} {ae} {bc} { bd} {be} {cd} {ce} {de} {abc} { abd} {ade} {bcd} { bce} {bde} {cde} {abcd} {abce} {acde} {bcde} To chyba będzie wszystko

wredulus_pospolitus: ogólnie: 2^{liczba elementów} ponieważ tworząc podzbiór każdy element ma 'dwie możliwości' (albo jest w podzbiorze albo nie jest) Więc będziemy mieli: a) 2⁴ = 16 −−−> więc zapomniałeś o jednym ... o {abd} b = 2⁵ = 32 −−−> więc zapomniałeś o aż o czterech ... o {abe}, {acd}, {ace} i o {abde}

wredulus_pospolitus: można też zauważyć, że liczba podzbiorów k−elementowych zbioru n−elementowego jest równa

	n k

Czyli dla (b):

	5 0
0 elementowych mamy:		= 1

	5 1
1 elementowych mamy:		= 5

	5 2
2 elementowych mamy:		= 10

	5 3
3 elementowych mamy:		= 10

	5 4
4 elementowych mamy:		= 5

	5 5
5 elementowych mamy:		= 1

Dzięki temu też od razu widać którego 'rodzaju' podzbiorów Ci brakuje i w jakiej ilości

Klasa 6 : Bardzo dziękuje za wytłumaczenie Muszę bardziej uważać przy wypisywaniu Zaraz sobie to wydrukuje

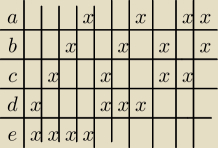
wredulus_pospolitus: Jeżeli upierasz się przy wypisywaniu wszystkich możliwych podzbiorów to warto sobie ułatwić w tą sprawę. 1. Zauważ, że podzbiory można połączyć w pary −−− w każdej parze podzbiory nie będą miały żadnego wspólnego elementu a ich suma da nam pełen zbiór (wyjściowy). 2. Zrobić tabelki tego typu: gdzie 'x' oznacza 'nie wybrane' elementy w podzbiorach 3 elementowych ... oraz wybrane elementy w podzbiorach 2 elementowych Dzięki temu łatwiej będzie się nie zgubić jakiś podzbiorów.

Klasa 6 : Nie upieram się zbytnio przy tym . W poleceniu było tez żeby je wypisać Ta tabelka ułatwi sprawę