wredulus_pospolitus:
Mamy sprawdzić czy istnieje możliwość aby: a
1 = a
2 ∧ b
1 = b
2.
Obalimy to dla trójkąta prostokątnego poprzez 'dowód nie wprost' (czyli zakładamy, że zachodzą
te równości i dojdziemy do sprzeczności, która powoduje 'zawalenie' się całej tezy).
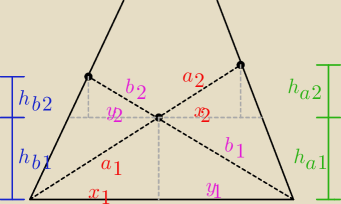
1. prowadzimy równoległą do podstawy trójkąta (AB), przechodzącą przez punkt O.
2. prowadzimy prostopadłe do podstawy z punktów K,M,O. Otrzymujemy w ten sposób cztery
trójkąty prostokątne o bokach (a
1, x
1, h
a1), (a
2, x
2, h
a2), (b
1, y
1, h
b1),
(b
2, y
2, h
b2)
3. na mocy 'odpowiedniego twierdzenie' o kątach odpowiadających oraz korzystając z założenia,
że a
1 = a
2 oraz b
1 = b
2 widzimy, że odpowiednie pary trójkątów są trójkątami
przystającymi.
4. Związku z tym, h
a2 = h
a1 oraz h
b2 = h
b1 oraz z oczywistego względu: h
a1 =
h
b1 (bo reprezentują wysokość tego samego punktu nad tą samą podstawą trójkąta).
5. jak również mamy: x
1 = x
2 oraz y
1 = y
2
6. skoro mamy tutaj do czynienia z trójkątem ostrokątnym, to wiemy, że y
1 > x
2 jak również,
że x
1 > y
2
ale przecież mamy y
1 = y
2 oraz x
1 = x
2 więc y
1 > x
2 ⇔ y
2 > x
1 a mamy dokładnie
w drugą stronę nierówność
sprzeczność i 'pozamiatane'.
Dla trójkąta prostokątnego będzie analogicznie, tylko tam w (punkcie 6) będzie (przykładowo)
x
2 = y
1 oraz x
1 > y
2 co doprowadzi do tej samej sprzeczności.
Teraz mam nadzieję, że widzisz dlaczego ten dowód nie wprost dla trójkąta rozwartokątnego
(gdzie kąt rozwarcia jest np. przy wierzchołku B) nie będzie działać
wredulus_pospolitus:
o cholera ... zmieniam swoją odpowiedź −−− nie można tak dobrać K i M aby zachodziło to co jest
podane w pytaniu.
A sam dowód jest jest stosunkowo prosty.
0. Korzystamy z tego samego rysunku
1. − 4. te same punkty
5. Związku z tym, że h
b1 + h
b2 = h
a1 + h
a2 to wiemy, że KM || AB
6. Czyli ABMK jest trapezem
gdzie AM i BK są przekątnymi tegoż trapezu.
7. Należy teraz pokazać (i to już Tobie zostawię, nie wymaga to specjalnych obliczeń, tylko
zauważenia trójkątów przystających) jeżeli punkt przecięcia przekątnych dzieli te przekątne na
połowy, to tenże trapez będzie niczym innym jak równoległobokiem
8. A skoro mamy równoległobok to AK || BM więc ich przedłużenia nigdy się nie przetną w
wierzchołku C ... więc trójkąt ABC nie istnieje.
sprzeczność i po sprawie
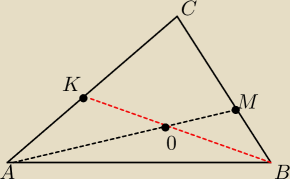W trójkącie ABC punkt K leży na boku AC a punkt M leży na boku BC
Odcinki AM i BK przecinają się w punkcie O
Czy może sie zdarzyć ze punkt O dzieli odcinki BK i AM na połowy ?