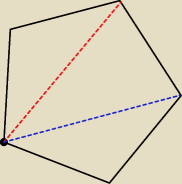
Wielokąt Mu Qi: Twierdzenie : Każdy wielokąt wypukły można podzielić na trójkąty Dowód : Żądany podział otrzymuje się wyberając jeden z wierzchołków wielokata i prowadząc wszystkie przekątne z niego wychodzące Jest zadane pytanie Dlaczego w tym dowodzie przekątne nie mogą sie przeciąć ? Kazali też sprawdzic na kilku rysunkach czy to twierdzenie jest słuszne dla wielokątów niewypukłych . Uczyniłem to i jest słuszne dla wielokątów wklęsłych

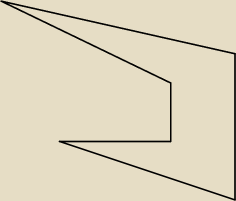
wredulus_pospolitus: Przekątna −−− odcinek łączący dwa różne wierzchołki wielokąta. Przekątne poprowadzone z jednego tego samego wierzchołka mają już jeden 'punkt wspólny'. Pytanie do Ciebie: Kiedy dwa odcinki mają dokładnie dwa punkty wspólne? Skoro uważasz, że dla niewypukłych też to 'gra' to zaproponuj podział w tym przypadku.

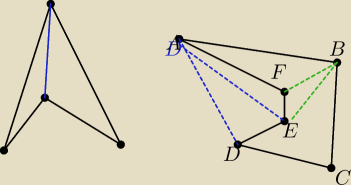
Mu Qi: Może tak Intuicja mi podpowiada że dwa odcinki mają dokladne dwa punkty wspolne gdy koniec jednego odcinka jest jednocześnie początkiem drugiego Mam napisane w książce ze to twierdzenie jest prawdziwe dla wszystkich wielokątów również niewypukłych Zrobiłem to dla takiego wielokąta wklęsłego Do Twojego zrobiłbym tak np Z A takie przekątne , Z B takie przekątne . Na razie nie mam napisane tego w książce że wielokąt wypukły można podzielić na (n−2) trójkątow (gdzie n to liczba boków Czy taka sama zasada działa na wielokąt wklęsły? Tego nie wiem Naprawdę

ite: 18:26 Jeśli dwa odcinki mają punkty wspólne, to albo dokładnie jeden albo nieskończenie wiele (taka geometria jest omówiona w Twoim podręczniku).

Mu Qi: Dobry wieczór. Dobrze. A problem z podziałem na te trójkąty wielokąta wklęłego tego co dał wredulus to zrobiłem dobrze?

ite: 18:26 zaproponowany podział wielokąta z prawej trzeba poprawić, bo figura BEDC nie jest trójkątem, trzeba ją jeszcze podzielić. A przekątne AE i AD usunąć, bo "kroją" powietrze a nie wielokąt. Zakładam, że podział wielokąta zdaniem autora podręcznika oznaczał dzielenie wnętrza figury a nie jej zewnętrza. Jeszcze zapytam, czy twierdzenie z 17:06 nie miało postaci: Każdy wielokąt wypukły można podzielić na trójkąty o wspólnym wierzchołku, który jest zarazem wierzchołkiem wielokąta ?

Hua Liulu: Dzień dobry Jest tak w książce https://zapodaj.net/plik-jrlDB6KWhF

ite: OK, w dowodzie jest mowa o przekątnych wychodzących ze wspólnego wierzchołka.

. : Ogólnie − kazdy wielokąt (wklesly lub wypukły) można podzielić na trójkąty korzystając z przekątnych (i boków) tego wielokąta. Co można łatwo wykazać indukcyjnie, Jednak tutaj mozwa była o przekątnych po prowadzonych z jednego (wybranego) wierzchołka i ta sprawa już nie jest możliwa w przypadku niektórych wielokątów wkleslych, co za prezentowałem przykładem z wczoraj.