13. Układ współrzędnych Hua Liulu: W podręczniku nie mam nic opisane oprócz tego jak narysować punkt w przestrzeni Jaka figure w przestrzeni określają warunki a) z=0 b) x=y i z=0 c) x=1 i y=3 d) |y|=|x|

. : Mówimy o układzie 3 współrzędnych?

. : Jeśli tak to mamy: 1. Płaszczyznę (równoległa od płaszczyzny Oxy) 2. Prosta. (leżącą na płaszczyźnie Oxy) 3. Prosta. (prostopadła do płaszczyzny Oxy) 4. Dwie przecinajace się pod kątem prostym płaszczyzny będące prostopadle do płaszczyzny Oxy

Hua Liulu: Tak . O układzie 3 wpółrzednych Tyle mam na temat przestrzeni w podręczniku https://zapodaj.net/plik-aQsehWoXoy

Hua Liulu: https://zapodaj.net/plik-FWKNr63aSr Póżniej wyskakuje z takimi zadaniami . Trudne dla mnie Dziękuje za odpowiedz .

Hua Liulu: Zadanie nr 143−145 zrobiłem W zadaniu nr 147 wspólna cecha to jednakowe współrzedne x i z Ale jak to bedzie linia ?

. : W 147 wszystkie trzy punkty leżą na jednej płaszczyźnie. Z treści zasłania wychodzi ze są wspoliniowe, zapomnij na moment o pierwszej współrzędne − masz punkty z dwoma wspolrzednymi (myśl o układzie 2 wymiarowym) jak wtedy wyznaczałes wzór prostej mając 2 punkty? Uczyń tak samo i tutaj

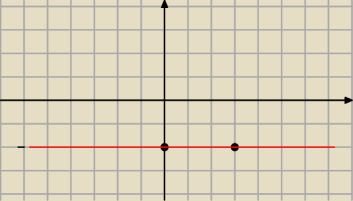
Hua Liulu: Jeszcze tego nie ma ale pamiętam (y−y₁)(x₂−x₁)=(y₂−y₁)(x−x₁) mamy A=(1,0,−2) B=(1,3,−2 ) Zapominam o 1 wspołrzednej A)0,−2) B(3.−2) (y−y₁)(x₂−x₁)−(y₂−y₁)(x−x₁)=0 Tutaj dostane y=−2 zrobiłem rysunek

Hua Liulu: J ęślli teraz weżme C(−50,−2) to także yen punkt bedzie należął do prostej y=−2

Hua Liulu: na tej linii będa leżec punkty które maja współrdzedne x=1 y−różne z=−2

. : No i widzisz... masz zadanie 'zrobione'. Jaki wniosek z tego − należy najpierw zrozumieć problem, następnie zastanowić się w jaki sposób można uprościć sobie tenże problem, rozwiązać uproszczona wersję i powrócić z tym do swojego problemu.

. : Teraz wróć do zadania 146 i postaraj się go rozwiązać poprzez 'zejście do 2 wymiarow' i zastanowienie się co wtedy by było prezentowane (gdybyśmy zapomnieli o jednej z osi współrzędnych)

mat: Skaczesz po działach,jak konik polny po łące

Hua Liulu: Dobrze . Postaram się to zrobić .

Hua Liulu: mat ,nie skacze. Opuścilem tyllko dwa działy z ksiązki 1)Działąnia w zbiorze liczb wymiernych i 2) Zbiory ograniczone

Hua Liulu: Zadanie nr 146 a) z=0 na płaszczyznie rownane x=0 lub y=0 określa oś OY lub oś OX Dlaczego to bedzie tak w przestrzeni że to plaszczyzna ?

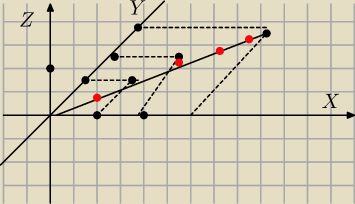
Hua Liulu: To do b) To będzie prosta i leży na płaszczyznie OXY

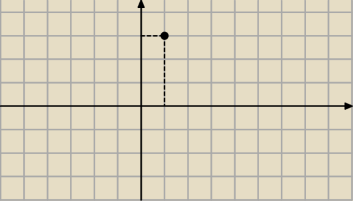
Hua Liulu: W d) na plaszczyznie |y|=|x| sa to dwie przecinające sie proste pod katem prostym Więc w przestrzeni to dwie przecinające sie płaszczyzny Natomiast w c) na płaszczyznie x=1 i y=3 to jest punkt natomiast nie bardzo rozumiem dlaczego w przestrzeni to jest prosta

. : To zamiast osi Oxy zrób oś Oxz (na przykład). Co wtedy będzie?

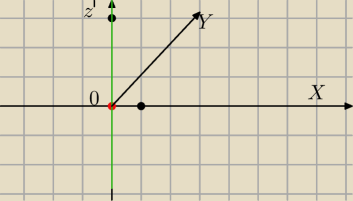
Hua Liulu: Jeśli wezme tak jak sugerujesz to wtedy bede miał tak x=1 , y=0 z=3 w przestrzeni będe miał ta zieloną prostą Wtedy jest to oś OZ i ona jest prostopadła do plaszczyzny OXY

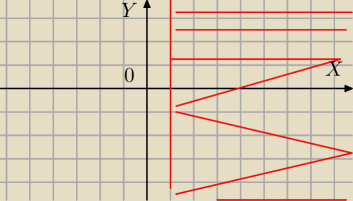
Lord Ding: Jaki zbiór w przestrzeni określaja nierówności a) x≥1 Na płaszczyżnie bedzie wyglądać to tak tak patrze na sciane w pokoje i wygląda mi na to że to będzie połpłaszczyzna równoległa do plaszczyzny OZY

Hua Liulu: b) −3≤x≤−2 na płaszczyznie bed\zie to pas A co w przestrzeni?

Hua Liulu: jeszcze mam takie coś c) 0≤x≤1 i 0≤y≤1 sa to pasy Tutaj na płaszczyznie OXY wychodzi mi kwadrat jako część wspolna d) −1≤x≤2, −2≤y≤1 i 3≤z≤6

Hua Liulu: Ktoś napisze. Dziękuje