Wartośc bezwzględna
Susu:
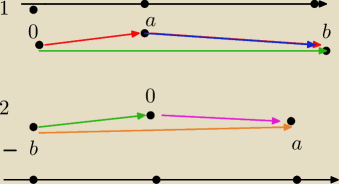
Ćwiczenie nr 58
Napisz wszystkie nierówności trójkata dla punktów na osi o współrzędnych a,b,0 oraz a,−b,0
Zaznaczyłem sobie tak zeby byłoby mi łatwiej odczytać
Do 1 na rysunku
Myśle tak
Długość odcinka \0a\=|a\
Długośc odcinka |0b|=|b|
Natomiast długość odcinka |ab|=|b−a|=|−(a−b)|=|a−b| bo |−x|=|x|
Więc będe miał takie nierówności trójkąta
|a|+|a−b|≥b
|b|+|a−b|≥|a|
|a|+|b|≥|a−b|
Do nr 2 na rysunku
Długośc odcinka |0(−b)|=|b|
Długośc odcinka |0a|=|a|
Długośc odcinka |(−b)a|=|a−(−b)|=|a+b|
Będe miał takie nierówności trójkąta
|b|+|a|≥|a+b| albo |a|+|b|≥|a+b|
|b|+|a+b|≥|a|
|a|+|a+b|≥b
czy tak będzie dobrze ?
Na razie tyle do tego ćwiczenia potem będe miał dalsze pytania o ile będzie dobrze Dziękuje
23 sie 11:35
ite:
Czy autorom podręcznika nie chodzi o nierówności ostre i o zbudowanie trójkątów
niezdegenerowanych?
Np. równobocznych albo równoramiennych (jako bliskich sercu każdego ucznia)?
23 sie 11:57
Susu:
dzień dobry ite
Za chwile wyślę skan ćwiczenia z działu Wartość bezwzględna
Potem następne ćwiczenie gdzie pytają o sens geometryczny
23 sie 12:03
Susu:
https://zapodaj.net/plik-GlB8Zag1Ct
Dostałem ta nierówność o której dalej pisze
|a|+|b|≥|a+b| czyli
|a+b|≤|a|+|b|
tam pisze o szacowaniach
A jaki będzie sens geometryczny (ćwiczenie nr 59 )
Bo potem w zadaniu nr 106 mam zastosowac to właśnie ćwiczenie nr 58
23 sie 12:13
Susu:
Prześpię sie z tym problemem i potem napisze co wymyśliłem
23 sie 14:00
Susu:
Milu
Prosze wytłumacz mi to ćwiczenie 59
Z tym zapisem przedziałow za pomocą wartości bezwzględnej juz doszłem jak bo on tam zrobił
kolizje zapisów
23 sie 20:48
Susu:
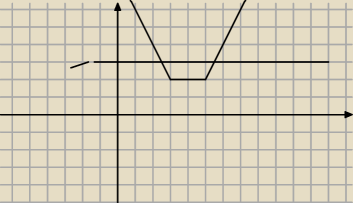
Mam np tak
|x−k|=t⇔k−t lub k+t
|x−5|=2 to x=3 lub x=7
Szukam takich x które sa odlegle o 2 od sroka k=5
gdy mam |x+k|=t to wtedy |x−(−k)|=t ⇔ (−k)−t lub −k+t
tak samo będzie z nierownością postaci |x−k|<t ⇔k−t<x<k+t
Chcemy dodac teraz dwa przedziały zapisane za pomoca wartości bezwzgłednej
|x−3|+|x−5|=3
||x−3|+|x−5||=|x−3|+|x−5| =3
Srodek 1 przedziału to a=3 środek drugiego przedziału to b=5
czyli mamy przedział <3,5> . ma byc =3 to 3 należy do tego przedziału wiec będa rozwiazania
Jeszcze zrobie wykres
Nie wiem czy dobrze to rozumiem
23 sie 21:11
Susu:
Jednak to ćwiczenie nr 59 jest dla mnie ważne
23 sie 21:14
Mila:

|a−3|≤1 i |b−3|≤1 ⇔
−1≤a−3≤1 /+3
2≤a≤4
analogicznie otrzymasz dla |b−3|≤1 przedział [2,4]
Obie liczby: a i b leżą w przedziale [2,4]
Co zapiszesz |a−b|≤2
23 sie 23:06
Susu:
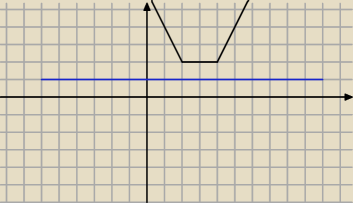
Dobrze. dziękuje

Wezmy to zadanie nr 106a)
|x−2|+|4−x|=1
|x−2|=1
x=1 lub x=3
|4−x|=1
|−(x−4)|=|x−4|=1 to x=3 lub x=5
Co dalej Milu mam robić?
jak zrobie wykres to nie ma rozwiążan
23 sie 23:37
Susu:
Po prostu jeden przykład żebym miał rozwiązany to skończe to zadanie .
Resztę zadań zrobie sam
23 sie 23:42
a:
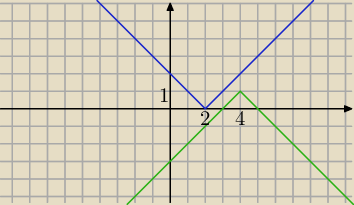
|x−2|= −|x−4|+1
graficznie
y=|x−2|
y= −|x−4|+1
Odp: brak rozwiązań
24 sie 00:14
Susu:
Dzięki bardzo za rozwiązanie

Mam jednak tam konkretne polecenie aby wykorzystać to ćwiczenie
24 sie 00:22
Mila:
Susu Wyjaśnię później co autor miał na myśli. Trochę mąci

( Smażę pomidory)
24 sie 15:30
Susu:
Dobrze. Nie ma sprawy .Poczekam .

Także bym zjadł trochę smażonych pomidorów . Teraz zajadam sie ogórkami
24 sie 15:46
Mila:
zadanie nr 106a)
Wyjaśnię to w skrócie
|x−2|+|4−x|=1
1) |x−2|+|4−x|≥|x−2+4−x|=2
To oznacza, że wyrażenie (|x−2|+|4−x|) ma najmniejszą wartość równą 2 i jest ona osiągana
dla x∊[2,4]
dla pozostałych wartości x ma wartości większe od 2.
Równanie :
|x−2|+|4−x|=1 nie ma rozwiązania
To widać na wykresie z godziny 00: 14. Autor nie proponuje uczniom takiego wykresu ,
bo wykresy będą w dalszym okresie edukacji.
2)
Równanie: |x−2|+|4−x|=2 ma nieskończenie wiele rozwiązań
Każda liczba x∊[2,4] spełnia to równanie
3)
Równanie: |x−2|+|4−x|=a, gdzie a>2 ma dwa rozwiązania
24 sie 18:43
Susu:
Mam to ]F[Milu]]

Dziękuję
24 sie 20:17
 Ćwiczenie nr 58
Napisz wszystkie nierówności trójkata dla punktów na osi o współrzędnych a,b,0 oraz a,−b,0
Zaznaczyłem sobie tak zeby byłoby mi łatwiej odczytać
Do 1 na rysunku
Myśle tak
Długość odcinka \0a\=|a\
Długośc odcinka |0b|=|b|
Natomiast długość odcinka |ab|=|b−a|=|−(a−b)|=|a−b| bo |−x|=|x|
Więc będe miał takie nierówności trójkąta
|a|+|a−b|≥b
|b|+|a−b|≥|a|
|a|+|b|≥|a−b|
Do nr 2 na rysunku
Długośc odcinka |0(−b)|=|b|
Długośc odcinka |0a|=|a|
Długośc odcinka |(−b)a|=|a−(−b)|=|a+b|
Będe miał takie nierówności trójkąta
|b|+|a|≥|a+b| albo |a|+|b|≥|a+b|
|b|+|a+b|≥|a|
|a|+|a+b|≥b
czy tak będzie dobrze ?
Na razie tyle do tego ćwiczenia potem będe miał dalsze pytania o ile będzie dobrze Dziękuje
Ćwiczenie nr 58
Napisz wszystkie nierówności trójkata dla punktów na osi o współrzędnych a,b,0 oraz a,−b,0
Zaznaczyłem sobie tak zeby byłoby mi łatwiej odczytać
Do 1 na rysunku
Myśle tak
Długość odcinka \0a\=|a\
Długośc odcinka |0b|=|b|
Natomiast długość odcinka |ab|=|b−a|=|−(a−b)|=|a−b| bo |−x|=|x|
Więc będe miał takie nierówności trójkąta
|a|+|a−b|≥b
|b|+|a−b|≥|a|
|a|+|b|≥|a−b|
Do nr 2 na rysunku
Długośc odcinka |0(−b)|=|b|
Długośc odcinka |0a|=|a|
Długośc odcinka |(−b)a|=|a−(−b)|=|a+b|
Będe miał takie nierówności trójkąta
|b|+|a|≥|a+b| albo |a|+|b|≥|a+b|
|b|+|a+b|≥|a|
|a|+|a+b|≥b
czy tak będzie dobrze ?
Na razie tyle do tego ćwiczenia potem będe miał dalsze pytania o ile będzie dobrze Dziękuje
 Mam np tak
|x−k|=t⇔k−t lub k+t
|x−5|=2 to x=3 lub x=7
Szukam takich x które sa odlegle o 2 od sroka k=5
gdy mam |x+k|=t to wtedy |x−(−k)|=t ⇔ (−k)−t lub −k+t
tak samo będzie z nierownością postaci |x−k|<t ⇔k−t<x<k+t
Chcemy dodac teraz dwa przedziały zapisane za pomoca wartości bezwzgłednej
|x−3|+|x−5|=3
||x−3|+|x−5||=|x−3|+|x−5| =3
Srodek 1 przedziału to a=3 środek drugiego przedziału to b=5
czyli mamy przedział <3,5> . ma byc =3 to 3 należy do tego przedziału wiec będa rozwiazania
Jeszcze zrobie wykres
Nie wiem czy dobrze to rozumiem
Mam np tak
|x−k|=t⇔k−t lub k+t
|x−5|=2 to x=3 lub x=7
Szukam takich x które sa odlegle o 2 od sroka k=5
gdy mam |x+k|=t to wtedy |x−(−k)|=t ⇔ (−k)−t lub −k+t
tak samo będzie z nierownością postaci |x−k|<t ⇔k−t<x<k+t
Chcemy dodac teraz dwa przedziały zapisane za pomoca wartości bezwzgłednej
|x−3|+|x−5|=3
||x−3|+|x−5||=|x−3|+|x−5| =3
Srodek 1 przedziału to a=3 środek drugiego przedziału to b=5
czyli mamy przedział <3,5> . ma byc =3 to 3 należy do tego przedziału wiec będa rozwiazania
Jeszcze zrobie wykres
Nie wiem czy dobrze to rozumiem
 |a−3|≤1 i |b−3|≤1 ⇔
−1≤a−3≤1 /+3
2≤a≤4
analogicznie otrzymasz dla |b−3|≤1 przedział [2,4]
Obie liczby: a i b leżą w przedziale [2,4]
Co zapiszesz |a−b|≤2
|a−3|≤1 i |b−3|≤1 ⇔
−1≤a−3≤1 /+3
2≤a≤4
analogicznie otrzymasz dla |b−3|≤1 przedział [2,4]
Obie liczby: a i b leżą w przedziale [2,4]
Co zapiszesz |a−b|≤2
 Dobrze. dziękuje
Dobrze. dziękuje  Wezmy to zadanie nr 106a)
|x−2|+|4−x|=1
|x−2|=1
x=1 lub x=3
|4−x|=1
|−(x−4)|=|x−4|=1 to x=3 lub x=5
Co dalej Milu mam robić?
jak zrobie wykres to nie ma rozwiążan
Wezmy to zadanie nr 106a)
|x−2|+|4−x|=1
|x−2|=1
x=1 lub x=3
|4−x|=1
|−(x−4)|=|x−4|=1 to x=3 lub x=5
Co dalej Milu mam robić?
jak zrobie wykres to nie ma rozwiążan
 |x−2|= −|x−4|+1
graficznie
y=|x−2|
y= −|x−4|+1
Odp: brak rozwiązań
|x−2|= −|x−4|+1
graficznie
y=|x−2|
y= −|x−4|+1
Odp: brak rozwiązań
 Mam jednak tam konkretne polecenie aby wykorzystać to ćwiczenie
Mam jednak tam konkretne polecenie aby wykorzystać to ćwiczenie
 ( Smażę pomidory)
( Smażę pomidory)
 Także bym zjadł trochę smażonych pomidorów . Teraz zajadam sie ogórkami
Także bym zjadł trochę smażonych pomidorów . Teraz zajadam sie ogórkami
 Dziękuję
Dziękuję