
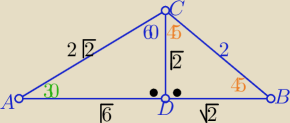
 Dwa złączone trójkąty "ekierkowe" spełniają treść zadania
i po ptokach
Dwa złączone trójkąty "ekierkowe" spełniają treść zadania
i po ptokach
 https://www.bryk.pl/pytania/pozostale/matematyka/6310-dany-jest-trojkat-o-bokach-2-2-pierwiastek-2-i-pierwiastek-2-pierwiastek-6-suma-miar-dwoch.html
https://www.bryk.pl/pytania/pozostale/matematyka/6310-dany-jest-trojkat-o-bokach-2-2-pierwiastek-2-i-pierwiastek-2-pierwiastek-6-suma-miar-dwoch.html
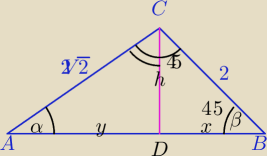 Sposób ABC jest błyskotliwy. Jeśli się nie wpadnie to trzeba popracować.
Na pewno znasz tw.Pitagorasa.
1) sprawdzasz czy Δ jest prostokątny− Nie.
2)
Szkic Δ, najdłuższy odcinek rysujesz jako podstawę
a)
x+y=√6+√2
y2+h2=8
x2+h2=4
======= (−)
y2−x2=4⇔(y−x)*(y+x)=4
b)
(y−x)*(√6+√2)=4 /*(√6−√2)
4(y−x)=4(√6−√2)
c)
y−x=√6−√2
y+x=√6+√2
=====(+)
⇔
y=√6 i x=√2, h=√2
Dalej już prosto.
Sposób ABC jest błyskotliwy. Jeśli się nie wpadnie to trzeba popracować.
Na pewno znasz tw.Pitagorasa.
1) sprawdzasz czy Δ jest prostokątny− Nie.
2)
Szkic Δ, najdłuższy odcinek rysujesz jako podstawę
a)
x+y=√6+√2
y2+h2=8
x2+h2=4
======= (−)
y2−x2=4⇔(y−x)*(y+x)=4
b)
(y−x)*(√6+√2)=4 /*(√6−√2)
4(y−x)=4(√6−√2)
c)
y−x=√6−√2
y+x=√6+√2
=====(+)
⇔
y=√6 i x=√2, h=√2
Dalej już prosto.
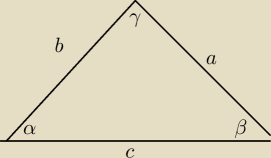 a=2
b=2√2
c=√2+√6=√2(1+p{3| jesli potrzebne będzie
Korzystam z tego ze w trojkącie naprzeciwko większego boku leży większy kąt
Wystarczy policzyć αi β bo γ=180o−(α+β(
a=2
b=2√2
c=√2+√6=√2(1+p{3| jesli potrzebne będzie
Korzystam z tego ze w trojkącie naprzeciwko większego boku leży większy kąt
Wystarczy policzyć αi β bo γ=180o−(α+β(
| (2√22+(√2+√6)2−22 | ||
cosα= | ||
| 2*2√2(√2+√6) |
| 8+8+2√12−4 | √3 | |||
cosα= | =......... = | |||
| 8+4√12 | 2 |
 nareszcie po 2 dniach, 12 godzinach i 52 minutach od mojej wskazówki natrafiono na ten prosty
choć rzemieślniczy lecz niezawodny sposób rozwiązania zagadki
nareszcie po 2 dniach, 12 godzinach i 52 minutach od mojej wskazówki natrafiono na ten prosty
choć rzemieślniczy lecz niezawodny sposób rozwiązania zagadki 