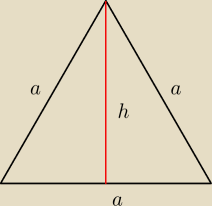
Odcinki niewspółmierne Fairy and Devil: W trójkącie rownobocznym chemy wykazać niewspółmirność wysokości z bokiem trójkąta o długości a=1

	m		m
Wobec tego |h|=		*|a|i i m.n ∊C i		nieskracalny
	n		n

Z twierdzenia Pitagorasa

	3
|h|2=||a|2−|1/2a|2=		|a|2
	4

m2		3
	*|a|2=		|a|2
n2		4

m2		3
	=
n2		4

	3n2
m2=
	4

Nie wiem jak to teraz uzasadnic

Saizou : Niech bok trójkąta wynosi 2a, wówczas h = a√3 Chcemy pokazać, że nie istnieje odcinek, który mieści się całkowitą liczbę razy w 2a oraz h. Załóżmy, że taki odcinek istnieje. Nazwijmy go d, wówczas a√3= m*d, m∊Z 2a = k*d, k∊Z,

√3		m
	=
2		k

	2m
√3 =		sprzeczność, bo lewa strona jest niewymierna a prawa wymierna.
	k

WNIOSEK: Odcinki 2a oraz a√3 są niewspółmierne

Fairy and Devil: Dzięki wielkie Chciałem to zrobić jak tutaj https://zapodaj.net/plik-3QFLTKyZhY