Geometria płaska
Mr. Ninja: Hejka, potrzebuję pomocy w trzech zadankach.
1. Dane są dwa okręgi o(O1, R), o(O2, r) styczne wewnętrznie R > r. Znaleźć promień
okręgu stycznego do tych okręgów oraz do prostej na której leżą średnice obu okręgów.
2. Dane są dwa okręgi o(O1, r), o(O2, R), gdzie |O1O2| = d (d > 0). Obliczyć długość
wspólnej stycznej zewnętrznej x oraz wspólnej stycznej wewnętrznej y.
3. W trójkącie ABC punkt D należy do boku AC i |AD| : |DC| = 1 : 3, na boku BC
dany jest punkt E taki, że |CE| : |EB| = 4 : 1. Punkt F jest punktem przecięcia odcinków BD i
AE. Oblicz pole trójkąta ABC wiedząc, że pole trójkąta ACF jest równe 2.
19 sie 10:13
Mr. Ninja: Poproszę o dokładne wyjaśnienia

19 sie 10:14
Kiwosz: Również potrzebował bym odpowiedzi do tych zadań. Proszę o dokładne wyjaśnienia
19 sie 14:16
Fairy and Devil:
Do zadania nr 2 to zadaj sobie najpierw pytanie
Kiedy dwa okregi maja styczna zewnetrzną i wewnetrzna ?
Znajdz sobie konstrukcje tych stycznych . do tych okręgów Dużo wyjaśni
Najpierw zrób to i pokaż obliczenia
19 sie 14:53
Mr. Ninja: Nie rozumiem co oznacza pojęcie "styczna zewnętrzna x" i "styczna wewnętrzna y". Jakbym mógł
poprosić o przykładowy rysunek w obydwu sytuacjach
19 sie 15:51
Kiwosz:
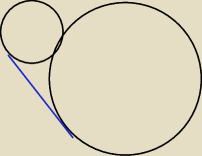
Niebieskim kolorem oznaczyłem styczną zewnętrzną, ale nie jestem w stanie znaleźć stycznej
wewnętrznej. Proszę o objaśnienie
19 sie 16:07
19 sie 16:24
Min. Edukacji: Aż w trzech

To załóż 3 posty

19 sie 16:28
Kiwosz: @www W zadaniu nie jest jasno powiedziane że |O1 O2| > R + r, stąd nie można jednoznacznie
określić czy styczna wewnętrzna istnieje
19 sie 19:22
Kiwosz: 
19 sie 19:23
Mila:
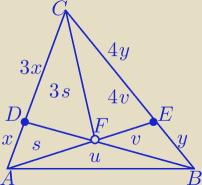
Zad.3
1)
ΔACE: ΔABE
| 4s+4v | | 4 | |
| = |
| ⇔4s=4u⇔s=u⇒ |
| v+u | | 1 | |
⇔3s=5v
2)
==============
19 sie 20:23
Fairy and Devil:
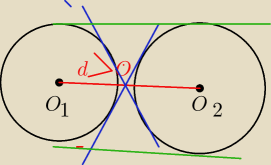
W zadaniu masz powiedziane ze odlegość srodkó okręgów d>0
Więc tylko w tej sytuacji okręgi będa miały styczną zewnetrzna (zielone −obie róne ) i styczną
wewnętrzna (niebieskie −obie równe)
19 sie 20:25
Fairy and Devil:
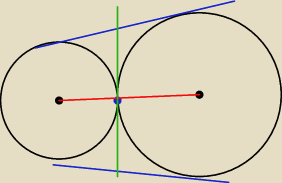
Taka sytuacja
O
1O
2=d=R
1+R
2
Są trzy styczne
2 zewnętrze niebieskie i jedna zielona
Ale czy zielona jest wewnętrzna tutaj ? NIe przechodzi przez dwa punkty (tak jak niebieskie )
wiec nie liczysz jej długości
19 sie 20:32
Fairy and Devil:
Rysuj sobie polożienia okręgów i patrz jakie będą styczne
19 sie 20:34
Fairy and Devil:
Jestem teraz zablokowany na komputerze po prośbie o usunięcie postu o kasynie i wiec nie wyślę
Ci materiałow
19 sie 20:44
Kiwosz: Udało mi się obliczyć styczną zewnętrzną x w zadaniu 2.
L1 = √d2 + (R − r)2
19 sie 23:13
Mr. Ninja: Tylko co teraz z drugą?
19 sie 23:13
Mila:
20:23 Ma być :
[ABC]=4.
Widzę,
Mr.Ninja nie czyta rozwiązań. 
19 sie 23:22
Mr. Ninja: Mila, czytam, czytam i jestem bardzo wdzięczny

19 sie 23:34
żółwik:
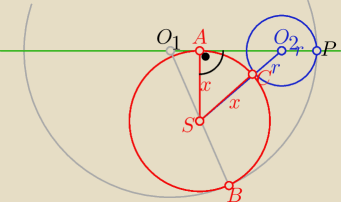
x−− dł. promienia szukanego okręgu ( z treści zadania)
|O
1P|=|O
1B|=R, |O
2P|=|O
2C|=r
|SO
s|=r+x , |SA|=x , |O
1S|= R−x , |AO
2|=y to: |O
1A|= R−y−r
z tw. Pitagorasa
wΔASO
2 i w ΔASO
1
1) x
2+y
2=(x+r)
2 i 2) x
2+(R−y−r)
2=(R−x)
2
rozwiązując ten układ równań ( wyznacz x z (1) i wstaw do (2)otrzymasz
odpowiedź ........
20 sie 11:54
Mr. Ninja:
żółwik
Pomocy, wychodzi takie coś:

−2Rr − 2R*
√2xr + r2 + r
2 +2r*
√2xr + r2 + 2xr + r
2 = − 2xR
20 sie 17:18
Fairy and Devil:
A tutaj w ogóle wyjdą pierwiastki?
20 sie 17:55
żółwik:
z (2) y
2+r
2−2Ry−2Rr+2yr=−2xR ( podstawiam za x i mnożę równanie przez r
i wszystko na prawą stronę
otrzymuję
(2) Ry
2+ry
2−2Rry+2r
2y −3Rr
2+r
3=0
grupuję
Ry
2+Rry −3Rry −3Rr
2+ry
2+r
2y +r
2y+r
3=0
Ry(y+r) −3Rr(y+r)+ry(y+r)+r
2(y+r)=0
(y+r)(Ry−3Rr+ry+r
2)=0
y= −r −− odrzucamy lub y(R+r)= 3Rr−r
2
to x=..........
dokończ bo już nie mam siły dalej pisać

Masz odp? bo mi wychodzi ( jak nie mam gdzieś po drodze błędu
Sprawdzaj
============
20 sie 18:17
żółwik:
Skąd wytrzasnąłeś te pierwiastki ?

20 sie 18:19
KvBa: Najpierw był y wyciągnięty i y = √2xr + r2
20 sie 20:14
kasacja:
? ?
21 sie 23:18

 Niebieskim kolorem oznaczyłem styczną zewnętrzną, ale nie jestem w stanie znaleźć stycznej
wewnętrznej. Proszę o objaśnienie
Niebieskim kolorem oznaczyłem styczną zewnętrzną, ale nie jestem w stanie znaleźć stycznej
wewnętrznej. Proszę o objaśnienie
 To załóż 3 posty
To załóż 3 posty

 Zad.3
Zad.3
 W zadaniu masz powiedziane ze odlegość srodkó okręgów d>0
Więc tylko w tej sytuacji okręgi będa miały styczną zewnetrzna (zielone −obie róne ) i styczną
wewnętrzna (niebieskie −obie równe)
W zadaniu masz powiedziane ze odlegość srodkó okręgów d>0
Więc tylko w tej sytuacji okręgi będa miały styczną zewnetrzna (zielone −obie róne ) i styczną
wewnętrzna (niebieskie −obie równe)
 Taka sytuacja
O1O2=d=R1+R2
Są trzy styczne
2 zewnętrze niebieskie i jedna zielona
Ale czy zielona jest wewnętrzna tutaj ? NIe przechodzi przez dwa punkty (tak jak niebieskie )
wiec nie liczysz jej długości
Taka sytuacja
O1O2=d=R1+R2
Są trzy styczne
2 zewnętrze niebieskie i jedna zielona
Ale czy zielona jest wewnętrzna tutaj ? NIe przechodzi przez dwa punkty (tak jak niebieskie )
wiec nie liczysz jej długości


 x−− dł. promienia szukanego okręgu ( z treści zadania)
|O1P|=|O1B|=R, |O2P|=|O2C|=r
|SOs|=r+x , |SA|=x , |O1S|= R−x , |AO2|=y to: |O1A|= R−y−r
z tw. Pitagorasa
wΔASO2 i w ΔASO1
1) x2+y2=(x+r)2 i 2) x2+(R−y−r)2=(R−x)2
rozwiązując ten układ równań ( wyznacz x z (1) i wstaw do (2)otrzymasz
odpowiedź ........
x−− dł. promienia szukanego okręgu ( z treści zadania)
|O1P|=|O1B|=R, |O2P|=|O2C|=r
|SOs|=r+x , |SA|=x , |O1S|= R−x , |AO2|=y to: |O1A|= R−y−r
z tw. Pitagorasa
wΔASO2 i w ΔASO1
1) x2+y2=(x+r)2 i 2) x2+(R−y−r)2=(R−x)2
rozwiązując ten układ równań ( wyznacz x z (1) i wstaw do (2)otrzymasz
odpowiedź ........
 −2Rr − 2R*√2xr + r2 + r2 +2r*√2xr + r2 + 2xr + r2 = − 2xR
−2Rr − 2R*√2xr + r2 + r2 +2r*√2xr + r2 + 2xr + r2 = − 2xR
 Masz odp? bo mi wychodzi ( jak nie mam gdzieś po drodze błędu
Sprawdzaj
Masz odp? bo mi wychodzi ( jak nie mam gdzieś po drodze błędu
Sprawdzaj
