Liczby wymierne i niewymierne na osi Fairy and Devil:

	m
Znajdz takie całkowite m aby punkt o współrzędnej		leżał wewnątrz odcinka o końcach
	8

	9
A=(−
	7

	8
B=(−
	7

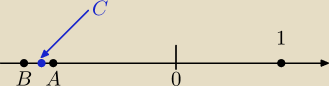
Odcinek |01| dzielę na 7 równych części i odkładam na osi punkt A i C Mam znależć taki punkt C żeby leżał pomiedzy punktami A i B Z tego wychodzi że m ∊C− Może trzeba znależć wspolny mianownik dla 7 i 8? Tak będzie dobrze ?

Fairy and Devil: A i B ma być odwrotnie na rysunku bo B jest wieksze

Fairy and Devil: Mam tak

−72		m		−64
	<		{56}<
56		7m		56

	−70		10
z tego m=−10 ∊C bo		=−
	56		8

Powinno być OK

Fairy and Devil: Poprawie zapis

−72		7m		−64
	<		<
56		56		56

. : Ogólnie − wszystko ok. Można też zauważyć ze:

m		m
	>
n		n+1

Natomiast jeżeli m>n to

m+1		m
	>
n+1		n

Mozna przemnozyc przez (−1) te nierówności aby Ci się nie pomieszało (w końcu A i B są mniejsze od 0).

	−9		−9		−8
Wbioskujac z powyższych nierówności zapisuje:		<		<
	7		8		7

. : Ale byka zrobiłem... Jeszcze sie cholera nie obudziłem Ciekawe czy zauważysz gdzie dokładnie tego była zrobiłem.

Fairy and Devil: Tutaj juz Jeżeli m>n to

m+1		m
	<		np dla m=4 i n=3
n+1		n

5		4
	<		1,25<1,33
4		3