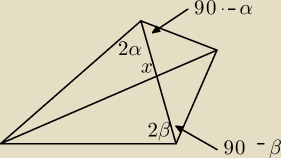
kąty chomik: Oblicz x wiedzac ze β−α=6^o

an: x=96^o

chomik: Akurat odpowiedź mam bo sprawdziłem w geogebrze tu plik: https://www.szybkiplik.pl/YvJ87T5fxi

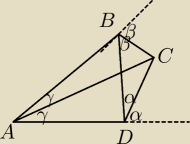
chomik: Jak wykażać że też AC jest dwusieczną

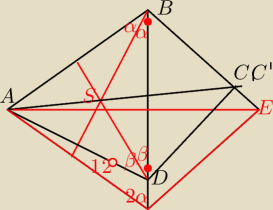
an: Kąty α i β z 10:07 Prosta ASC' jest dwusieczną, trzeba udowodnić, że C=C'. Udowodnienie, że suma kątów AC'B oraz AC'D równa jest kątowi BCD powinno wystarczyć, a to nie jest skomplikowane.

chomik: A możesz to pokazac bo nie bardzo rozumiem twój rysunek co tam jest dorysowanie☹️

an: Czerwone na dole to dla α=β, chociaż to miała być inna koncepcja ten rysunek "wysłał się sam" i niewiele wnosi. Resztę chyba rozumiesz, bo wiesz, że tam jest dwusieczna.

chomik: Niestety ale nadal nie wiem czemu AC jest dwusieczną

Sowa: A tak naprawde to czym jest x na rysunku? a) kątem? b) długością zaznaczonego odcinka? c) długościa krótszej przekatnej ?

an: Kąt ∡BCD=180−(90−α)−(90−β)=α+β

	180−2α−2β
∡AC'B=180−[		+2α+(90−α)]=β
	2

	180−2α−2β
∡AC'D=180−[		+2β+(90−β)]=α
	2

∡AC'B+∡AC'D=α+β=∡BCD, czyli .....punkt C jest tożsamy z C' ⇒ AC jest dwusieczną ∡BAD x=96^o

chomik: A można skorzystać z twierdzenia:Środek okręgu dopisanego do trójkąta jest punktem przecięcia się dwusiecznych kątów zewnętrznych przy wierzchołkach i dwusiecznej kąta wewnętrznego przy trzecim wierzchołku.

an: Można będzie bardzie "elegancko"

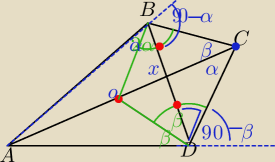
Mila: C− środek okręgu dopisanego do boku BD AC jest dwusieczną kąta A Czworokąt ODCB jest czworokątem cyklicznym x=β+90−α x=96^o

chomik: https://zapodaj.net/images/6edca17edd5b5.jpg

Mila: