Trygonometria okresowosc funkcji Zagubiona: W takim rownaniu: sin3x=cosx Dlaczego nie mozna zrobic tak: Skoro sinx=cosx dla x= π/4+kπ, kEZ To w przypadku sin3x=cosx 3x= π/4+kπ, kEZ / : 3 x= π/12+kπ/3, kEZ

. : Nieee

Sowa: Można zrobić wykres i na wykresie wyjdzie czy to jest prawda co napisałas sin(3x)= 3sin*(x)−4sin³(x) Ale ja bym robił tak

	π
cos(x)= sin(		−x)
	2

	π
sin(3x)= sin(		−x)
	2

	π
3x=		−x+2kπ
	2

	π		2
x1=		+		kπ drugie rozwiązanie
	6		3

x₂= π−x₁= ....

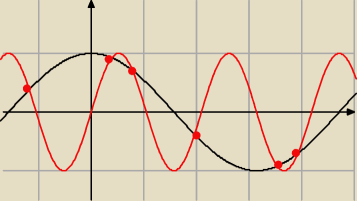
wredulus_pospolitus: tutaj masz zaznaczone punkty będące rozwiązaniem równania: sin(3x) = cosx

Sowa: Skopałem

	π
ma byc oczywiście 4x=		+2kπ
	2

to x₁= .......... x₂=π−x=.... Zauważyłem że nie przeniosłem x na lewą stronę

wredulus_pospolitus: @Sowa po pierwsze:

	π		kπ
3x = π/2 − x + 2kπ −−−> 4x = π/2 + 2kπ −−−> x =		+
	8		2

a takie podejście do sprawy (mimo że bardzo ciekawe) nie daje Ci wszystkich rozwiązań. Pytanie − czy wiesz dlaczego

Sowa: Myśle że wiem Napisałem że sa dwa rozwiązania tego równania drugie rozwiązanie to x₂=π−x Czy to jest dobre podejście do sprawy?

wredulus_pospolitus: nie do końca, bo będzie:

	π
x 2 =		+ kπ (patrz wykres)
	4

a tobie by wyszedł okres kπ/2

Sowa: Napisz proszę gdzie zrobiłem błąd . Zwrócę potem na to uwage . Dziękuje

Zagubiona: Okej, ale dlaczego nie mozna tak zrobic (tzn. podzielic przez 3 wlasnie)? Bo wiem ze mozna probowac innymi sposobami, ale zalezy mi na tym, zeby dowiedziec sie dlaczego ten jest zly, bez zadnych wykresow itp. Moze jakis warunek trzeba dac, ktory odrzucilby niektore z rozwiazan ktore wychodzą( a wychodza 4 i dwa z nich sa prawidlowe)?

Sowa: A możesz napisać swoje rozwiązanie tego równania z tymi czterema rozwiązaniami i ltóre z nich są prawidłowe?

Sowa: Ja także sie dopiero tego uczę Myślę tak Napisałaś kiedy sin(x)=cos (x) Dla innych argumentów oprocz tych sin(x)≠cos(x) więc nie można porównywać argumentów dwóch róznych funkcji Kiedy można będzie to zrobić ? Według mnie wtedy kiedy będziemy mieli do porównaia dwie te same funkcje Tutaj będzie nam łatwiej zamienić cos(x) na sin(x) Wtedy możemy juz porównać argumenty tych funkcji Jeśli to jest niestety złe myślenie to prosiłbym o poprawę Albo można zrobić tak to równanie sin(3x)=cos(x) sin(3x)=sin(π/2−x) sin(3x)−sin(π/2)−x)=0 wzór na sinα−sinβ=...... zobacz Dostaniesz postać a*b=0 więc a=0 lub b=0 Ale piszesz ze wiesz że można rozwiążac to sposobami wiec ufam ze to wiesz jak dalej A to dlaczego tak nie można to albo moje tłumaczenie jest OK albo pewnie ktoś poprawi jak złe .

Zagubiona: Chyba po prostu trzeba przyjac, ze to dziala wtedy, kiedy sin i cos maja ten sam argument, a twoje rozwiazanie z zamienieniem cosinusa na sinus jest faktycznie bardziej przejrzyste

Sowa: W książce Trygonometria dla samouków Edward Jerzy Pokorny na stronie 203 autor pisze tak ** Zapamiętajmy . Aby rozwiążać równanie trygonometryczne w którym występują odmienne funkcje ytrygonometryczne ,staramy się zawsze doprowadzić to równanie do takiej postaci żeby niewiadoma występowała w nim pod znakiem tylko jednej funkcji trygonometrycznej **