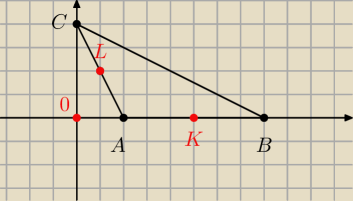
 A(p,0)
B(q,0)
C(0,h)
a) Znależć równanie okręgu opisanego na trójkącie ABC
b)Znależć równanie okręgu przechodzącego przez środek AB, spodek wysokości ΔABC z wierzchołka C
,środek AC
c)Sprawdż że okrąg otrzymany w b) przechodzi przez srodek BC
Czy ten rachunek można uznać za dowód twierdzenia:
Dla każdego trójkąta okrąg przechodzący przez środki boków przechodzi również przez spodki
wysokości
a)
x2−2ax+y2−2by+c=0
1)p2−2ap+0−0+c=0
2)q2−2aq+0−0+c=0
3)0−0+h2−2bh+c=0 (p≠0 q≠0 ih≠0 bo wtedy nie będzie to trójkąt.
{p2−2ap+c=0
{q2−2aq+c=0
{h2−2bh+c=0
Jak się zabrać za taki układ równań po kolei?
A(p,0)
B(q,0)
C(0,h)
a) Znależć równanie okręgu opisanego na trójkącie ABC
b)Znależć równanie okręgu przechodzącego przez środek AB, spodek wysokości ΔABC z wierzchołka C
,środek AC
c)Sprawdż że okrąg otrzymany w b) przechodzi przez srodek BC
Czy ten rachunek można uznać za dowód twierdzenia:
Dla każdego trójkąta okrąg przechodzący przez środki boków przechodzi również przez spodki
wysokości
a)
x2−2ax+y2−2by+c=0
1)p2−2ap+0−0+c=0
2)q2−2aq+0−0+c=0
3)0−0+h2−2bh+c=0 (p≠0 q≠0 ih≠0 bo wtedy nie będzie to trójkąt.
{p2−2ap+c=0
{q2−2aq+c=0
{h2−2bh+c=0
Jak się zabrać za taki układ równań po kolei?
| h2+pq | ||
x2+y2−(p+q)x− | *y+pq=0 | |
| h |