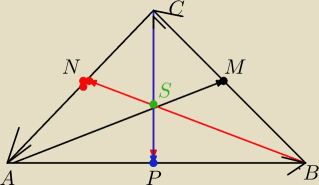
Niech A(x1,y1) B(x2,y2) C(x3,y3) będą wierzchołkami trójkąta
M,N,P środkami boków BC,CA i AB
Znajdz punkty dzielące wektory AM→,BN→CP → w stosunku k=2
Jakie twierdzenie o środkowych trójkąta wywnioskujesz z uzyskanego wyniiku?
| x2+x3 | ||
xM= | ||
| 2 |
| y2+y3 | ||
yM= | ||
| 2 |
| x2+x3 | y2+y3 | |||
M( | , | ) | ||
| 2 | 2 |
| (x1+x3 | y1+y3 | |||
N | , | ) | ||
| 2 | 2 |
| x1+x2 | y1+y2 | |||
P( | , | ) | ||
| 2 | 2 |
| x1+k*x2 | y1+k*y2 | |||
x= | y= | −−ogólne | ||
| 1+k | 1+k |
| x1+2*(x2+x3)/2 | x1+x2+x3 | |||
xS1= | = | |||
| 1+2 | 3 |
| y1+y2+y3 | ||
yS1= | ||
| 3 |
| x1+x2+x3 | y1+y2+y3 | |||
S1( | , | ) | ||
| 3 | 3 |
| x2+x1+x3 | ||
xS2= | ||
| 3 |
| y2+y1+y3 | ||
yS2= | ||
| 3 |
| x1+x2+x3 | y1+y2+y3 | |||
S2( | , | |||
| 3 | 3 |
| x3+x1+x2 | x1+x2+x3 | |||
xS3= | = | |||
| 1+2 | 3 |
| y3+y1+y2 | y1+y2+y3 | |||
yS3= | = | |||
| 3 | 3 |
| x1+x2+x3 | y1+y2+y3 | |||
S3( | , | ) | ||
| 3 | 3 |
