Zbiór wartości Sowa: Mam funkcje określona wzorem

	x2
f(x)=
	x2+1

D(f)=ℛ Mam określić jej zbiór wartości R(f) Bez obliczeń widzę ze R(f)= <0,1) A jak mam to wyznaczyć analitycznie ? Dziękuje

ite: Można w taki sposób: − przekształcenie wzoru wyjściowej funkcji

	x2		x2+1−1		1
f(x)=		=		=1−
	x2+1		x2+1		x2+1

− określenie zbioru wartości funkcji, która jest w mianowniku odjemnika dla x∊ℛ (łatwe : ) g(x)=x²+1 → R(g)=[ 1;+∞)

	1
− policzenie 1−		=0
	1

	1
oraz limx→+∞[1−		]=1
	x2+1

Sowa: Dziękuje bardzo

Sójka:

x2
	= y D=R
x2+1

yx²+y=x² (y−1)x²+y=0 Δ≥0 ⇔ −4y(y−1)≥0 ⇔y(y−1)≤0 y∊[0,1] ZW=[0,1]

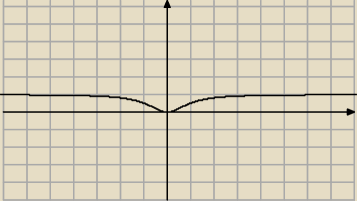
Sowa: Ale coś tu nie pasi bo ta funkcja nie osiągnie wartosci y =1

chichi:

	x2
równanie		= 1 jest sprzeczne − nie ma rozwiązań, zatem wartość równa 1 nie jest
	x2 + 1

osiągana przez funkcję f.

chichi:

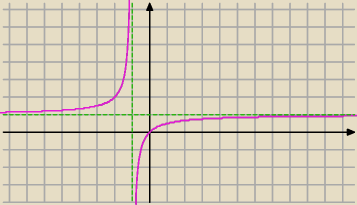
	x2
f(x) =		, połóżmy t = x2, t ≥ 0 i zbadajmy wykres funkcji
	x2 + 1

	t		1
g(t) =		= −		+ 1, i odczytujemy dla t ≥ 0 → [0,1) i to szukany ZWf
	t + 1		t + 1

Sowa: Dziękuje bardzo .

Mila: Jeśli rozwiązujesz sposobem Sowy to tak:

x2
	=w
x2+1

w− wartość f(x) x²=wx²+w x²−wx²=w x²*(1−w)=w badamy dla jakich wartości w równanie kwadratowe ma rozwiązanie a) 1−w=0⇔w=1 L=0 , P=1 sprzeczność b) w≠1

	w
x2=
	1−w

w
	≥0 ( parabola w*(1−w) skierowana dół )
1−w

w∊<0,1)

Sowa: Dziękuje Mila

Sójka: Zgubiłam założenie y−1≠0 ⇒ y≠1 ZW= [0,1)

Mila: Sójka , przestań kochać deltę, nie zawsze trzeba z niej korzystać.