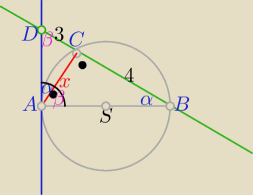
PLANIMETRIA kotuś: Odcinek 𝐴𝐵 jest średnicą okręgu o środku 𝑆. Prosta 𝑘 jest styczna do tego okręgu w punkcie 𝐴. Prosta 𝑙 przecina ten okrąg w punktach 𝐵 i 𝐶. Proste 𝑘 i 𝑙 przecinają się w punkcie 𝐷, przy czym |𝐵𝐶| = 4 i |𝐶𝐷| = 3 Odległość punktu 𝐴 od prostej 𝑙 jest równa?

kotek: 2√3

kotuś: to wiem, czy moglbys podac sposób z wykorzystaniem Pitagorasa?

kotuś: rozwiązałem zadanie sposobem wykraczającym za maturę podstawową, ale nie mam pomysłu jak może zrobić to osoba na takim poziomie

kotek: x²=4*3 x=2√3

kotuś: nie ma własnie tego w podstawie ///

kotek: Podobieństwo trójkątów ABC i ACD z cechy (kkk)

x		3
	=		⇒ x2=4*3
4		x

x=2√3 Podobieństwo jest w podstawie

kotuś: racja, zapomniałem ze wzór h=sqrt(ab) wyprowadza sie z prawdopodobienstwa

kotuś: podobieństwa*

kotek: 2 sposób z twierdzenia o stycznej i siecznej |AD|²=3*7 i z tw. Pitagorasa x²= |AD|²−3² x²=12 x=2√3