Algorytm jarnika vs kruskala
Szofer : Jaka jest różnica między tymi dwoma algorytmami ?
5 sie 22:06
Szofer : Bo czytam i ciężko jakoś wyczuć mi różnicę a do zadania mi potrzebne.
5 sie 22:16
. :
Ciężko? No to nie wiem. Ja jie miałem pojęcia o tych algorytm ach i zajęło mi 5 minut aby
zajarzyc jak one działają i czym się różnią w swojej zasadzie.
5 sie 22:43
Szofer : No ale w dwóch prostych słowach?
6 sie 09:26
Szofer : Poważnie się pytam.
6 sie 11:43
wredulus_pospolitus:
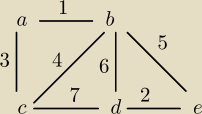
Jarnika −
1) wybieramy dowolny wierzchołek od którego będziemy prowadzić ścieżkę
2) wybieramy 'najtańszą' krawędź i dodajemy wierzchołek
3) oraz wszystkie krawędzie tego wierzchołka
4) wybieramy kolejną 'najtańszą' krawędź (o ile nie zamknie nam cyklu) i dodajemy kolejny
wierzchołek
powtarzamy krok (3) i (4) aż do momentu dodania ostatniego wierzchołka
Czyli : zaczynamy z dowolnego punktu i z tego punktu (wierzchołka) poprzez krawędzie
rozchodzimy się po całym grafie.
Kruskała −
1) SORTUJEMY krawędzie pod względem 'kosztu'
2) Zaczynamy od najtańszej krawędzi (co daj nam dwa wierzchołki)
3) Wybieramy kolejną najtańszą krawędź (nie musi być połączona z już wybranymi wierzchołkami),
o ile nie zamknie nam cyklu − wtedy daną krawędź omijamy
powtarzamy (3) krok aż do połączenia wszystkich wierzchołków.
Czyli: zaczynamy od najtańszych dróg i sukcesywnie je dodajemy do trasy, aż w końcu będziemy
mieli wszystkie wierzchołki
A. Jarnika:
1. Startujemy w dowolnym miejscu ... niech to będzie wierzchołek D.
2. Mamy krawędzie: DE, DB, DC (już są postortowane od najtanszej do najdroższej) .. wybieramy
DE
3. Dodajemy krawędź EB. Więc mamy EB,DB,DC ... wybieramy EB.
4. Dodajemy krawędzie AB i BC (krawędź BD już jest). Więc mamy AB, BC, DB, DC ... wybieramy AB.
5. Dodajemy krawędź AC. Więc mamy AC, BC, DB, DC ... wybieramy AC
co kończy pracę algorytmu
A. Kruskala
1. Sortujemy krawędzie od najtańszej do najdroszej: AC, DE, AC, BC, BE, BD, CD
2. Wybieramy najtańszą: AB −−− mamy już wierzchołki a i b
3. Wybieramy najtańszą: DE −−− mamy już 4 wierzchołki a, b, d, e
4. Wybieramy najtańszą: AC −−− mamy już 5 wierzchołków a, b, c, d, e
5. Pomijamy najtańszą BC, ponieważ zamknie nam się cykl (a,b,c)
6. Wybieramy najtańszą: BE −−− mamy już 5 wierzchołków POŁĄCZONYCH
co kończy pracę algorytmu
Teraz widzisz różnicę w pracy tych algorytmów

6 sie 12:13
wredulus_pospolitus:
Tak więc ... patrząc z podejścia informatycznego − kwestia kiedy sortujesz (i ile)
wierzchołków.
u Kruskała wszystkie krawędzie sortujesz na początku.
u Jarnika sortujesz ograniczoną liczbę krawędzi, a w kolejnych krokach sukcesywnie
'dosortowujesz' pozostałe
czy to ma jakiś wpływ na złożoność obliczeniową −−− nie mam pojęcia ... nie mój 'konik'.
6 sie 12:30
wredulus_pospolitus:
Dodatkowa różnica pomiędzy tymi algorytmami jest taka, że
u Kruskała 'wizja' ścieżki ścieżki może być widoczna dopiero na sam koniec podczas gdy u
Jarnika widzimy w kolejnych etapach jak kolejne wierzchołki są dodawane do spójnej całości.
6 sie 12:34
: 
6 sie 14:31
Szofer: Dziękuje. Bóg zapłać.
7 sie 19:35
Szofer: Jeszcze raz dzięki. W internetach jak patrzyłem to tak sobie było to wytłumaczone ale tutaj
daje już do myślenia. Dziękuje.
7 sie 19:43
Szofer: Pytałem o te różnice pomiędzy tymi algorytmami w kontekście tego zadania:
"Pewna firma zajmująca się transportem kolejowym prowadzi działalność w następujących miastach:
Szczecin, Gdańsk, Poznań, Bydgoszcz, Łódź, Wrocław, Gorzów Wielkopolski, Opole. Poglądową mapę
dostępnych tras kolejowych z dwukierunkowymi przelotami przedstawia rysunek poniżej
https://zapodaj.net/plik-iwIWQaAHAN .
Wyznacz najkrótszy możliwy czas(w minutach) transportu towarów ze Szczecina do Opola
zakładając, że pociągi poruszają się ze stałą szybkością 190 km/h na wszystkich odcinkach tras
i nie zatrzymują sie. Podaj również przebieg trasy tego transportu. Skorzystaj z
tabeli(tabela jest tu
https://zapodaj.net/plik-iwIWQaAHAN .)" Taki przelot trasy tych pociągów muszę zrobić tylko pomiędzy
miastami, które wymienione są w zadaniu?
8 sie 16:57
. :
Tak − ale ani jeden ani drugi algorytm nie jest właściwy dla tego zadania
8 sie 18:27
Szofer: Właśnie i myślałem jeszcze nad algorytmem djikstry?
8 sie 18:59
. :
Zamiast myśleć nad algorytmem to byś policzył te 4 drogi i porównał która jest najlepsza
8 sie 19:07
Szofer: No tak, ale musi tu być użyty jakiś algorytm. Jak inaczej zrobić to zadanie.
8 sie 19:47
wredulus_pospolitus:
to jedziesz tym djikstry (zmodyfikowanym)
8 sie 20:11
wredulus_pospolitus:
Jak to jak 'inaczej' ... normalnie policzyć na łapkach

Naprawdę już nic nie jesteś sam policzyć, o ile nie masz podanej procedury algorytmu (krok po
kroku co robić)

Jeżeli tak, to jak Ty sobie wyobrażasz programować cokolwiek?
8 sie 20:12
Szofer: Ale nie musisz się tak pieklić @wredulus. Staram się rozważyć wszystkie możliwe warianty. Może
ta matematyka nie jest moją mocną stroną ale staram się jakoś nad tym pracować.
8 sie 22:13
wredulus_pospolitus:
Szofer −−− dobrze jest znać algorytmy ... a raczej − kojarzyć że taki a taki jest i wiedzieć
gdzie szukać informacji o nim.
Jednak nie ma nic ważniejszego od umiejętności logicznego i analitycznego myślenia, rozłożenia
problemu na 'czynniki pierwsze' i znalezienia sposobu na rozwiązanie danego problemu.
Tak więc −−− zamiast pisać: "ale musi tu być użyty jakiś algorytm. Jak inaczej zrobić to
zadanie" ... powinieneś pisać: "muszę się zastanowić jak można podejść do tego zadania".
Nie wiem czy mnie rozumiesz −−− tu nie chodzi o to czy matematyka jest mocno czy słabą stroną
(w tym zadaniu to akurat 'mało tej matematyki jest') tu chodzi oto czy jesteś w stanie
'kombinować' i podchodzisz do problemu z hasłem "no dobra ... zobaczmy co tutaj można zrobić"
czy też zamykasz się i przeglądasz długą listę algorytmów i szukasz takiego który by w 100%
pasował do danego zadania.
8 sie 22:28
Szofer: No to mój sposób na rozwiązanie tego zadania jest taki. Mianowicie. Mam podane miasta:
Szczecin, Gdańsk, Poznań, Bydgoszcz, Łódź, Wrocław, Gorzów Wielkopolski, Opole. I jakbym
rozwiązał to zadanie to zrobiłbym bym to tak:
Mam wyznaczyć najkrótszą trasę ze Szczecina do Opola. No to zaczynam w punkcie startowym czyli
w Szczecinie i sprawdzam połączenia pomiędzy miastami, które są podane w zadaniu. Czyli
sprawdzam czy istnieje połączenie Szczecina, z którymś z podanych miast jeśli tak to wypisuje
odległość pomiędzy tymi miastami i tak robie z każdym z miast. Następnie sprawdzam najkrótsze
odległości i na tej podstawie tworze graf i wszystko ze sobą sumuje. Jak by było coś nie jasne
to powiedz to doprecyzuje.
10 sie 17:49
Szofer: Chyba że idąc twoim tokiem rozumowania mogę wyliczy @. : to chodzi ci o to że patrząc na ten
graf który tam jest mogę spojrzeć na poszczeglóne połączenia pomiędzy wymienionymi miastami i
wszystko zsumować. Nie wiem czy o to ci chodziło pisząc: "Zamiast myśleć nad algorytmem to byś
policzył te 4 drogi i porównał która jest najlepsza"
14 sie 17:56
wredulus_pospolitus:
Tak jak pisałem −−− możesz skorzystać z algorytmu który podałeś ... do tego on jest.
Albo zacznijmy od narysowania tego grafu prawidłowo 'w skali'
14 sie 19:32
Szofer: @wredulus __ pospolitus: pisząc " możesz skorzystać z algorytmu który podałeś" masz na myśli
to:
"patrząc na ten
graf który tam jest mogę spojrzeć na poszczeglóne połączenia pomiędzy wymienionymi miastami i
wszystko zsumować"
czy to co napisałem 10.08?
14 sie 21:31
wredulus_pospolitus:
chodzi mi o moją wypowiedź: to jedziesz tym djikstry (zmodyfikowanym)
14 sie 21:59
Szofer: Ok. A to co ja napisałem to można by wykorzystać do tego zadania czy nie? Tylko szczerze.
14 sie 22:28
Szofer: A co masz na myśli mówiąc że ten algorytm djisktry ma być zmodyfikowany. W jakim sensie?
16 sie 14:10
. :
Szofer − mam pytanie, Ty to już studiowałeś czy się przyuczasz do materiału którego jeszcze nie
miałeś?
16 sie 14:38
Szofer: Wykorzystywałem ten algorytm Djikstry, ale jak mam rozumieć "zmodyfikowany"? Rozwiązałem to
zadanie ale nie wiem czy zgodnie z ideą "zmodyfikowany". Dlatego pytam.
16 sie 16:32
Szofer: No to o co chodzi z tym zmodyfikowanym algorytmem djisktry. Wytłumaczy mi to ktoś? Bo
przerabiałem ten algorytm ale o zmodyfikowanym nie słyszałem przez co nie jestem pewien
rozwiązania.
17 sie 20:15
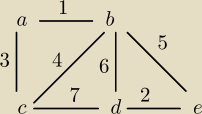 Jarnika −
1) wybieramy dowolny wierzchołek od którego będziemy prowadzić ścieżkę
2) wybieramy 'najtańszą' krawędź i dodajemy wierzchołek
3) oraz wszystkie krawędzie tego wierzchołka
4) wybieramy kolejną 'najtańszą' krawędź (o ile nie zamknie nam cyklu) i dodajemy kolejny
wierzchołek
powtarzamy krok (3) i (4) aż do momentu dodania ostatniego wierzchołka
Czyli : zaczynamy z dowolnego punktu i z tego punktu (wierzchołka) poprzez krawędzie
rozchodzimy się po całym grafie.
Kruskała −
1) SORTUJEMY krawędzie pod względem 'kosztu'
2) Zaczynamy od najtańszej krawędzi (co daj nam dwa wierzchołki)
3) Wybieramy kolejną najtańszą krawędź (nie musi być połączona z już wybranymi wierzchołkami),
o ile nie zamknie nam cyklu − wtedy daną krawędź omijamy
powtarzamy (3) krok aż do połączenia wszystkich wierzchołków.
Czyli: zaczynamy od najtańszych dróg i sukcesywnie je dodajemy do trasy, aż w końcu będziemy
mieli wszystkie wierzchołki
A. Jarnika:
1. Startujemy w dowolnym miejscu ... niech to będzie wierzchołek D.
2. Mamy krawędzie: DE, DB, DC (już są postortowane od najtanszej do najdroższej) .. wybieramy
DE
3. Dodajemy krawędź EB. Więc mamy EB,DB,DC ... wybieramy EB.
4. Dodajemy krawędzie AB i BC (krawędź BD już jest). Więc mamy AB, BC, DB, DC ... wybieramy AB.
5. Dodajemy krawędź AC. Więc mamy AC, BC, DB, DC ... wybieramy AC
co kończy pracę algorytmu
A. Kruskala
1. Sortujemy krawędzie od najtańszej do najdroszej: AC, DE, AC, BC, BE, BD, CD
2. Wybieramy najtańszą: AB −−− mamy już wierzchołki a i b
3. Wybieramy najtańszą: DE −−− mamy już 4 wierzchołki a, b, d, e
4. Wybieramy najtańszą: AC −−− mamy już 5 wierzchołków a, b, c, d, e
5. Pomijamy najtańszą BC, ponieważ zamknie nam się cykl (a,b,c)
6. Wybieramy najtańszą: BE −−− mamy już 5 wierzchołków POŁĄCZONYCH
co kończy pracę algorytmu
Teraz widzisz różnicę w pracy tych algorytmów
Jarnika −
1) wybieramy dowolny wierzchołek od którego będziemy prowadzić ścieżkę
2) wybieramy 'najtańszą' krawędź i dodajemy wierzchołek
3) oraz wszystkie krawędzie tego wierzchołka
4) wybieramy kolejną 'najtańszą' krawędź (o ile nie zamknie nam cyklu) i dodajemy kolejny
wierzchołek
powtarzamy krok (3) i (4) aż do momentu dodania ostatniego wierzchołka
Czyli : zaczynamy z dowolnego punktu i z tego punktu (wierzchołka) poprzez krawędzie
rozchodzimy się po całym grafie.
Kruskała −
1) SORTUJEMY krawędzie pod względem 'kosztu'
2) Zaczynamy od najtańszej krawędzi (co daj nam dwa wierzchołki)
3) Wybieramy kolejną najtańszą krawędź (nie musi być połączona z już wybranymi wierzchołkami),
o ile nie zamknie nam cyklu − wtedy daną krawędź omijamy
powtarzamy (3) krok aż do połączenia wszystkich wierzchołków.
Czyli: zaczynamy od najtańszych dróg i sukcesywnie je dodajemy do trasy, aż w końcu będziemy
mieli wszystkie wierzchołki
A. Jarnika:
1. Startujemy w dowolnym miejscu ... niech to będzie wierzchołek D.
2. Mamy krawędzie: DE, DB, DC (już są postortowane od najtanszej do najdroższej) .. wybieramy
DE
3. Dodajemy krawędź EB. Więc mamy EB,DB,DC ... wybieramy EB.
4. Dodajemy krawędzie AB i BC (krawędź BD już jest). Więc mamy AB, BC, DB, DC ... wybieramy AB.
5. Dodajemy krawędź AC. Więc mamy AC, BC, DB, DC ... wybieramy AC
co kończy pracę algorytmu
A. Kruskala
1. Sortujemy krawędzie od najtańszej do najdroszej: AC, DE, AC, BC, BE, BD, CD
2. Wybieramy najtańszą: AB −−− mamy już wierzchołki a i b
3. Wybieramy najtańszą: DE −−− mamy już 4 wierzchołki a, b, d, e
4. Wybieramy najtańszą: AC −−− mamy już 5 wierzchołków a, b, c, d, e
5. Pomijamy najtańszą BC, ponieważ zamknie nam się cykl (a,b,c)
6. Wybieramy najtańszą: BE −−− mamy już 5 wierzchołków POŁĄCZONYCH
co kończy pracę algorytmu
Teraz widzisz różnicę w pracy tych algorytmów 

 Naprawdę już nic nie jesteś sam policzyć, o ile nie masz podanej procedury algorytmu (krok po
kroku co robić)
Naprawdę już nic nie jesteś sam policzyć, o ile nie masz podanej procedury algorytmu (krok po
kroku co robić)  Jeżeli tak, to jak Ty sobie wyobrażasz programować cokolwiek?
Jeżeli tak, to jak Ty sobie wyobrażasz programować cokolwiek?