Równanie krzywej SuSu: Znależć równanie krzywej będącej zbiorem wszystkich cięciw AB paraboli y²=4x jeśki wiadomo nam ze proste łączące wierzchołek tej paraboli z punktami A B sa wzajemnie prostopadłe . Wykonać rysunek

. : A nie chodzi o krzywa będącej zbiorem SRODKOW wszystkich cięciw paraboli?

SuSu: Oczywiście tak

. : Zauważ że A, B i Wierzchołek będą leżały na okręgu któregeo średnica będzie ów cięcia AB, a środek okręgu będzie środkiem tejże cieciwy

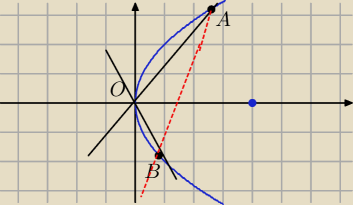
SuSu: na razie zrobiłem taki rysunek Jutro już będe liczył dalej bo i tak żeby obliczyć współrzedne srodka AB to musze obliczyć najpierw wspólrzedne punktów A i B

SuSu: Niech prosta OA ma równanie y=mx i m≠0

	1
To z warunku prostopadłości prostych równanie prostej OB będzie takie y=−		x i m≠0
	m

Obliczam wspólrzedne punktu A {y²=4x {y=mx m²x²=4x m²x²=4x=0 }

	4
x(m2x−4)=0 stąd xA=0 lub xA=
	m2

Pierwsze rozwiązanie odpada gdyz wtedy nie dostaniemy cięciwy tylko punkt

	4		4
Wobec tego yA= m*		=
	m2		m

	4		4
A=(		,		)
	m2		m

Obliczam współrzedne punktu B (y²=4x

	1
{y=−		x
	m

	x
(−		)2=4x
	m

x2
	=4x
m2

x²−4xm²=0 x(x−4m²)=0 stąd x_B=0 to rozwiązanie odpada lub x_B=4m²

	1
więc yB= −		*4m2= −4m
	m

Punkt B ma współrzedne B=(4m²,−4m²) Obliczam współrzedne srodka S=(x₀,y₀) cięciwy AB

	xA+xB		(4/m2)+4m		4		2		2+2m3
xs=		=		=		+2m=		+2m=		? (tu nie wiem
	2		2		2m2		m2		m2

czy OK )

	yA+yB		(4/m)−4m		2−2m2
ys=		=		=		to powinno być OK
	2		2		m

Tutaj prosiłbym o odpowiedż jak mam z tych zależnośći wyrugować m ?

SuSu: Natomiast w książce mam podane że

	2+2m4
xs=		ale chyba to bład w książce
	m2

Potem jest napisane Rugując z tych zależności m otrzymujemy y²_s= 2(x_s−4) Obliczenia muszę zrobić sam ale widzę że będzie to równanie paraboli o nowym wierzchołku O₁= (4,0)

SuSu: Ktoś napisze jak to wyrugować?

SuSu:

Mila: Punkt B ma współrzędne B=(4m²,−4m) 1)

	1		4		2
xs=		*(		+4m2)=		+2m2
	2		m2		m2

xs		1
	=		+m2
2		m2

	2
ys=		−2m,
	m

ys		1
	=		−m
2		m

2)

x		1		1		1
	=		+m2=(		−m)2+2*		*m}⇔
2		m2		m		m

x		1
	=(		−m)2+2
2		m

x		y
	−2=(		)2
2		2

x		y2
	−2=
2		4

y²=2x−8 y²=2*(x−4) ============

SuSu: Dzięń dobry Milu dlaczego współrzedne środka dzielisz przez 2?

Mila: Dla łatwiejszego "doprowadzenia " do zależności między x i y.

SuSu: Na razie Ci dziękuje