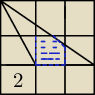
pole chomik: Kwadrat został podzielony na 9 taki samych kwadratów. Pole kazdego z tych kwadratów wynosi 2. Jak obliczyć pole "niebieskiej części?

Susu: Skoro P_pk=2 to bok pojedynczego kwadratu a_pk=√2 Teraz bym zastosował twierdzenie Pitagorasa

chomik: A gdzie zastosować to twierdzenie?

kerajs: Inaczej: Pole odciętego od niebieskiego kwadratu trójkącika to 1/12 pola tego kwadratu, więc szukane pole to 11/6.

chomik: A skąd 1/12 , da się to jakoś wytłumaczyć lub obliczyć innym sposobem?

kerajs: Skąd? Bo widać, że boki (przyprostokątne) odciętego trójkącika (prostokątnego) to 1/2 i 1/3 boku niebieskiego kwadratu.

chomik: Ja tego nie widze

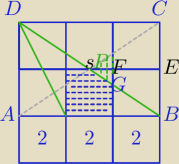
Mila: [ABCD]=12

	12
[BCS]=		=3
	4

|SE|=U{3√2}}{2}

	1		SF		1
|SF|=		√2⇔		=
	2		SE		3

	1		1
Pzielonego Δ=		*3=
	9		3

	1		1
[SFG]=		Pz.Δ=
	2		6

	1		11
Pn.=2−		=
	6		6

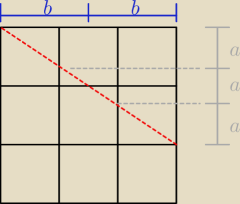
wredulus_pospolitus: Inny sposób:

	2
3a = 2√2 −−> a =		√2
	3

	3
2b = 3√2 −−> b =		√2
	2

Stąd wiemy, że trójkącik ma przyprostokątne:

	√2
1. b − √2 =
	2

	√2
2. √2 − a =
	3

	1		2		1
Stąd PΔ =		*		=
	2		2*3		6

	1		11
Więc Pzacieniowane = 2 −		=
	6		6

wredulus_pospolitus: PS. Zastosowane zostało tw. Talesa (a raczej − wnioski wynikające z tw. Talesa)