Rozwiązać nierówność lasso: √log_1/2 x +2 > log_1/2 x

kerajs: Podstawienie: t=log_1/2x przekształca nierówność w √ t+2 > t

Mila: Nie zapomnij o założeniach.

Susu: A także o tym że podstawa logarytmu jest w przedziale (0,1) więc zmieni sie zwrot nierówności Tak mi się wydaje

Fairy and Devil:

Fairy and Devil: Założenia zrobiłbym takie 1) x>0 2) log{1/2)x+2≥0 log_1/2x+log_1/24≥log_1/21 log_1/24x≥log_1/21 4x≤1

	1
x≤
	4

	1
x∊(−∞,		> −0
	4

Proszę sprawdzić czy dziedzina dobrze wyznaczona

chichi: log_0.5(x) ≥ log_0.5(4) ⇔ x ≤ 4 @Fairy and Devil log_0.5(4) = −2 ≠ 2

chichi: i nie zapisałeś jak wygląda dziedzina, tylko warunki. dziedziny jeszcze tam nie ma wyznaczonej

Fairy and Devil: Dzięki za poprawienie Załozenia zrobiłem takie 1) liczba logarytmowana x >0 2) To co pod pierwiastkiem ≥0 Wobec tego czego jeszcze brakuje ?

chichi: chodziło mi o to, że dziedziną jest cześć wspólna zbiorów, które, zostały wyznaczone w poszczególnych warunkach, aby podać dziedzinę należy jeszcze wszystko zebrać do kupy

Fairy and Devil: Zaraz sobie poprawię . dzięki

lasso: Jak podstawiam t=log{1/2}x, wychodzi mi, że √ t+2 > t, podnoszę obustronnie do kwadratu przy założeniach, że t = <0, +oo) rozwiązując nierówność kwadratową otrzymuje, że t == (−1,2), łącząc z założeniami => t = <0,2) i podstawiając potem log_1/2x

lasso: Jak podstawiam t=log_1/2x, wychodzi mi, że √ t+2 > t, podnoszę obustronnie do kwadratu przy założeniach, że t = <0, +oo) rozwiązując nierówność kwadratową otrzymuje, że t == (−1,2), łącząc z założeniami => t = <0,2) i podstawiając potem log_1/2x >= 0 i log_1/2x < 2 x<= 1 x> ¹₄ i ostatecznie wychodzi, że x = ( ¹₄ , 1> (już z dziedziną) jednak w odpowiedzi jest od (¹₄, 4> proszę o pomoc

Fairy and Devil: dziedzina z założeń wychodzi x∊(0,4> Po podstawieniu log₁/1}x=t i t∊ℛ masz do rozwiazania nierówność t²−t−2<0 stad t₁=−1 t₂=2 więc t∊(−1,2) Wracamy do podstawienia log_0,5x=−1 (czy to jest prawdziwe ?

	1
log0,5x=2 to x=
	4

Więc z tego juz z dziedzina mamy ze x∊(1/4,4> Możesz sobie to sprawdzic biorąc końce przedziału Proszę także bardzo uważać na zapisy log_ax=t t∊R log²_ax=t t≥0 Według mnie przedział rozwiązań należy zapisać przy pomocy symbolu (∊) a nie symbolu (=)

ite: Dlaczego o 18:00 uwzględniasz jedynie t ∊ <0, +∞) ? ← taki powinien być poprawny zapis A pomijasz t ∊ (−2;0) ?

lasso: A skąd wynika, że t ∊ (−2;0)? Moja nierówność wygląda tak √t +2 > t Z tego co uczyłem się, to przed podniesieniem do kwadratu należy napisać założenia więc t +2 >= 0 i t >= 0 t >= − 2 Biorąc część wspólną wychodzi mi, że t >= 0, czyli t ∊ (0;+oo) Czy gdzieś tutaj jest błąd? Skąd wychodzi, że t ∊ (−2;0) ?

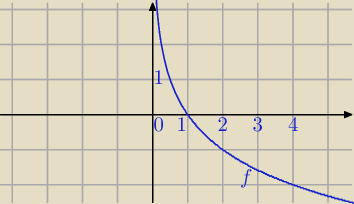
Mila: Pomoże wykres funkcji w ustaleniu prawidłowej odpowiedzi ? f(x)=ln_(1/2)(x)− prawa strona nierówności

ite: Jeśli stosujesz podstawienie t = log_1/2(x) , to z wykresu Mili można wywnioskować, że t∊ℛ. Teraz trzeba rozwiązać nierówność √t+2>t, więc należy ograniczyć t do liczb spełniających nierówność t+2≥0. Czyli t ∊ [−2;∞). Analizujemy dwa przypadki: 1/ t ∊ [−2;0) Wtedy lewa strona nierówności jest nieujemna a prawa ujemna, więc nierówność jest prawdziwa dla każdej liczby z tego przedziału. 2/ t ∊ [0, +∞) i to jest ten przypadek, gdy obie strony nierówności są nieujemne, więc podnosisz stronami do kwadratu i dalej rozwiązujesz równanie kwadratowe. I oba te przypadki w sumie dają rozwiązanie z odpowiedzi w podręczniku czyli (1/4; 4].

ite: lasso przy ewentualnym podnoszeniu nierówności stronami do kwadratu lepiej patrzeć w innej kolejności: − zacząć od spojrzenia, jakie wartości przyjmuje zmienna (żeby potem pamiętać o całej dziedzinie i niczego nie pominąć), − ustalić, dla których wartości zmiennej obie strony nierówności mają ten sam znak i wtedy podnosić do kwadratu (jeśli to pomoże znaleźć rozwiązania), − zastanowić się, co w przypadku tych wartości zmiennej, gdy strony nierówności mają różne znaki.

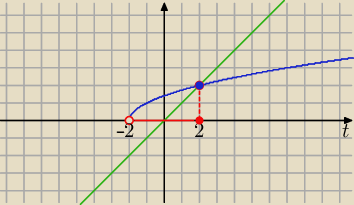
aso: graficznie ...( ładnie widać) log_1/2x =t , t∊R √t+2>t y=√t+2 y=t t∊(−2,2] −2<log_1/2x≤2

	1
x∊(		,4]
	4