trójkat
MLOX: W trójkącie ABC kąt BAC=20o oraz 3√a3+b3+c3−3abc=min{b,c}. Wykaż ze ABC jest
równoramienny.
20 lip 09:44
ite:
Czy a, b, c to długości boków?
20 lip 13:05
MLOX: Tak naprzeciwko wierzchołków
20 lip 13:17
MLOX:
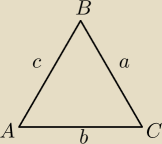
20 lip 13:28
ABC:
jest taka tożsamość w trójkącie dowolnym:
a
3cos(B−C)+b
3cos(C−A)+c
3cos(A−B)=3abc
wydaje mi się że z niej coś by poszło, ale wakacje są nie chce mi się myśleć

20 lip 13:57
kikus: Wyrażenie 3√a3+b3+c3−3abc jest symetryczne, ponieważ zmiana b przez c nie zmienia jego
wartości. Jeśli b i c nie są równe, nie możemy powiedzieć, że takim wyrażeniem jest, więc b=c
i trójkąt jest równoramienny.
21 lip 16:46
ABC:
gdzie wykorzystałeś założenie o kącie 20 stopni ?

21 lip 17:56
wredulus_pospolitus:
kikus −−−− i co z tego

To nie oznacza że jeden z boków nie może być krótszy od drugiego.
22 lip 01:26
kikus: ok tak teraz to widze, sorry za to
22 lip 09:51
Fairy and Devil:
Witam pytanko
Co oznacza zapis min(b,c) w wyrażeniu 3√a3+b3+c3=min(b.c)?
Dziękuje
22 lip 18:37
mat: minimum z b i c zapewne
22 lip 18:46
Fairy and Devil:
Mat
Tak naprawdę to tego nie rozumiem .
Jeśli chodzi o funkcje to gdy były np dwie funkcje i był określony jakiś przedział to przy
minimum brało sie pod uwagę funkcję której wykres był powiedzmy niżej polożony w układzie
wspólrzędnych
Tutaj to tak naprawdę nie wiem o co chodzi w tym zadaniu
22 lip 19:40
wredulus_pospolitus:
Jak to nie wiemy o co chodzi?
Wiemy, że krótsze z ramion (przyjmujemy, że a −−− długość podstawy) trójkąta będzie spełniała
tą równość ... i tyle.
Nie wiemy ile będzie wynosiła długość dłuższego ramienia. Nie wiemy ile wynosi długość
podstawy.
Znamy kąt oraz wiemy, że krótsze ramię spełnia tą równość. Na tej podstawie trzeba pokazać, że
'dłuższe' ramie także spełnia tą równość −−− co w efekcie daje nam, że jest to trójkąt
równoramienny.
22 lip 20:09
wredulus_pospolitus:
poprawka −−− max(b,c) =
3√...... <−−−− tą równość ma spełniać 'dłuższe' ramie

22 lip 20:10
Fairy and Devil:
Dobrze
22 lip 21:03



 To nie oznacza że jeden z boków nie może być krótszy od drugiego.
To nie oznacza że jeden z boków nie może być krótszy od drugiego.
