Prostopadłość w przestrzeni uczeń geometrii przestrzennej: Uzasadnij że w prostopadłościanie o krawędziach podstawy 3 i 5 i wysokości 4 przekątne są prostopadle. Jak to zrobić? Twierdzenie o 3 prostych z tego działu ale jak robię rzuty przekątnych na plaszyczne podstawy to wcale nie widzę że te rzuty są prostopadle

wredulus_pospolitus: Skoro podstawą jest PROSTOKĄT (który nie jest kwadratem), to rzuty przekątnych na płaszczyznę podstawy NIE BĘDĄ prostopadłe Nie ma takiej możliwości.

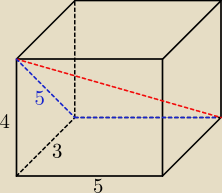
wredulus_pospolitus: zauważ, że zaznaczony trójkąt jest trójkątem prostokątnym, równoramiennym ... i teraz ... albo z długości boków (pamiętaj, że przekątne przecinają się w połowach swych długości) bądź z kątów wykażesz, że są one prostopadłe

uczeń geometrii przestrzennej: No właśnie nie widzę co dalej 😭

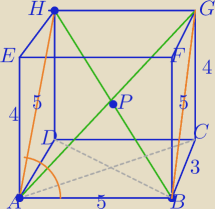
Mila: 1) W ΔADH: Z tw. Pitagorasa AH=5 AH=AB 2) Rozważmy przekątne: AG i HB ΔBAH − Δprostokątny równoramienny ponieważ krawędź AB ⊥(pł. ADHE ) i przebija ją w punkcie A to jest prostopadła do każdej prostej z (pł.ADHE) przechodzącej przez punkt A. (Na rysunku masz AD, AH,AE) AB⊥AH z T_3⊥ |HB|=5√2=|AG| AP=PH Oczywiście można HB obliczyć z tw. Pitagorasa w ΔHDB, prostopadłość HD i DB wynika z def. prostopadłościanu i T_3⊥ HD⊥(pł. ABCD) to HD⊥DB − (T_3⊥) 3)

	5√2
|AP|=|PH|=
	2

I teraz np. Tw. odwrotne do tw. Pitagorasa w ΔAPH Dokończ Jeśli masz pytanie , to pisz.

promując_geogebrę: dodaję model od oglądania z różnych stron https://www.geogebra.org/m/rdha6qh5

k: Przekrój ABGH jest kwadratem bo |AB|=|AH|=|BG|=|GH|=5 Przekątne kwadratu są prostopadłe koniec dowodu

Mila: Wydawało mi się, że autor chciał "widzieć" twierdzenie o 3 prostopadłych. (T_3⊥) Mogli dać trudniejszy przykład. Chyba, że to sama napisałaś zadanie koleżanko z 19:10.

an: Z treści zadania moim zdaniem wynika, że wszystkie przekątne są między sobą prostopadłe co nie jest prawdą czy nie należy tego zamieścić w odpowiedzi

Mila: Masz rację an. Uczeń nic już nie pisze. Nie wiadomo czy treść jest dokładnie taka jak napisał. Ma podpowiedzi, w tym w geogebrze, a k podpowiada, że wystarczy spojrzeć na odpowiedni przekrój.

uczeń geometrii przestrzennej: Dziękuję Mila. Sprawdź jak możesz później moje 3 nowe tematy