Równanie krzywej Fairy and Devil: Znajdz równanie krzywej będących zbiorem środków wszystkich cięciw paraboli y²=2x i przechodzących przez punkt (1,0)

: Wklepujemy w Gugle i .. https://forum.zadania.info/viewtopic.php?t=41701 https://matematyka.pl/viewtopic.php?t=60867 itd. itp. tylko trochę trzeba jeszcze pomyśleć

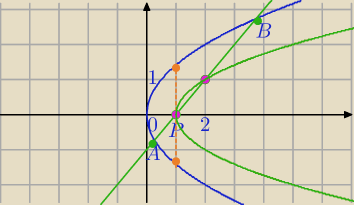
Mila: prosta AB: y=ax+b, x≥0, P∊prostej y=ax−a ⇔y=a(x−1) Punkty wspólne z parabolą y²=2x a²(x−1)²=2x a²x²−2(a+1)x+a²=0 Δ≥0 ( Jeden środek już mamy − to punkt P) Δ=4(a+1)²−4a⁴>0

	1−√5		1+√5
⇔a∊<		,		>
	2		2

Nie szukamy rozwiązań lecz skorzystamy z wzorów Viete'a , aby obliczyć wsp. środków cięciw

x1+x2		(a+1)
	=
2		a2

y1+y2		ax1−a+ax2−a		a(x1+x2)−2a		a(x1+x2)
	=		=		=		−a
2		2		2		2

	y1+y2		a(a+1)
⇔		=		−a
	2		a2

Zbiór punktów:

	(a+1)		a(a+1)		1−√5		1+√5
<		,		−a> dla a∊<		,		>
	a2		a2		2		2

y²=x−1 ? może jakiś błąd rachunkowy zdarzył się. Sprawdź rachunki.

Fairy and Devil: Dziękuje bardzo. Sprawdzę.

: a2x2−2(a²+1)x+a2=0 ale dalej wychodzi, że 2a²≥−1

Mila: Dziękuję za poprawkę, zgubiłam dwójkę w potędze. Brak precyzji z mojej strony. Δ jest nieujemna dla każdego a∊R. Zaraz będę poprawiać. A może autor poprawi rachunki? Metoda pozostaje.

małoletni Fairy: Można też tak: y²=2x , x≥0 i P(1,0)∊k

	y+a
k: y=ax−a ⇒ x=		, a≠0
	a

	y+a
to y2=2*
	a

ay²−2y−2a=0 Δ= 4+8a² >0

	y1+y2		1		x1+x2		1
		=		to		=		+1
	2		a		2		a2

	1		1
Zbiór środków cięciw z treści zad : <		+1,		> dla a≠0
	a2		a

należy do paraboli y²= x−1 Rysunek jak u Mili

Mila: W moim rozwiązaniu po usunięciu usterki : 1) a) Prosta AB: y=ax+b, x≥0, P=(1,0)∊prostej y=ax−a ⇔y=a(x−1) a≠0 b) Dla a= 0 nie ma puntu przecięcia Mamy prostą x=1, która ma dwa punkty przecięcia z podaną parabolą (1,0) − środek cięciwy Punkty wspólne z parabolą y²=2x a²(x−1)²=2x a²x²−2(a²+1)x+a²=0 Δ=4(a²+1)²−4a⁴ Δ≥0 (a²+1)²−a⁴≥0 (a²+1−a²)*(a²+1+a²)≥0 2a²+1>0 dla a∊R 2) Współrzędne środków cięciw:

x1+x2		2(a2+1)		a2+1
	=		=
2		2a2		a2

y1+y2		ax1−a+ax2−a		a(x1+x2)−2a
	=		=
2		2		2

y1+y2		1
	=
2		a

Zbiór środków cięciw:

	1		1
{(1+		,		),(1,0)}, a≠0
	a2		a

Teraz spróbuj sam ustalić wzór krzywej