całki - obszar m: Dany jest obszar Ω={(x,y)∈R²: |x|+|y|≤1} oraz odwzorowanie f:(x,y)→(x−y, 2x+2y). Ile wynosi pole powierzchni obrazu f(Ω)? Bardzo proszę o rozpisanie tego zadania od początku do końca. Dużo czasu minęło kiedy ostatni raz robiłam tego typu zadania

kerajs: Znajdź obrazy wierzchołków przekształcanego kwadratu (czyli (0,1), (1,0), (−1,0) i (0,−1)) i oblicz pole uzyskanego czworokąta.

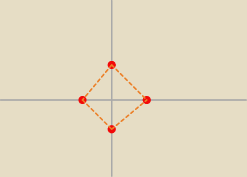
m: Ok, czyli pole powierzchni obrazu f(Ω) wynosi: 2, i to jest odpowiedź? Po co w zadaniu jest to odwzorowanie? Jak otrzymać te punkty?

ite: 2 to pole obszaru Ω wyznaczonego warunkiem z 14:30, my mamy policzyć pole powierzchni obrazu tego obszaru w przekształceniu f. Punkty z 09:57 wyznaczają obszar Ω (tworzą kwadrat). Te punkty zostały wyznaczone na podstawie własności |x|+|y|≤1}. Teraz musisz znaleźć współrzędne obrazów tych punktów po przekształceniu f, tak jak pisze kerajs. Otrzymasz inny czworokąt, będący obrazem obszaru Ω w przekształceniu f czyli f(Ω). I to właśnie jego pole jest odpowiedzią w tym zadaniu.

m: Czyli dla punktów (0,1), (1,0), (−1,0) i (0,−1) obrazami są: (−1, 2)(1,2)(−1,−2)(1,−2) I pole po narysowaniu punktów na wykresie wynosi 8. Czy teraz to jest dobrze?

ite: tak