równanie i parametr rzeczywisty pati: Cześć, jak radzić sobie z takimi zadaniami? https://ibb.co/QPN1c9D Nie chodzi mi tu nawet o ten konkretny przypadek, ale o ogólny typ zadania z parametrem. Jeśli chodzi o I i III pytanie to myślę, że mogę podstawić m i spróbować rozwiązać. Nie wiem, jak się zabrać za inne pytania, gdzie jest napisane "wtedy i tylko wtedy".

chichi: można równanie zapisać równoważnie |x² + 4x| − 2x = m², teraz niech f(x) = |x² + 4x| − 2x, narysować wykres funkcji f i odczytywać te własności

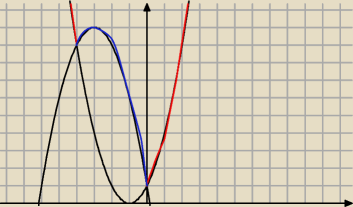
wredulus_pospolitus: Najczęściej tego typu zadania najprościej rozwiązać .... graficznie. L = |x²+4x| −2x + 1 dla x ∊ (−4;0) L = −(x² + 4x) − 2x + 1 = −x² − 6x + 1 = − x² − 6x − 9 + 10 = −(x+3)² + 10 dla x ∉ (−4;0) L = x² + 4x − 2x + 1 = x² +2x + 1 = (x+1)² mając wykres szybko można zauważyć −−− że: b) 1 rozwiązanie będzie dla P = 1 −−−> m²+1 = 1 −−−> m = 0 (wtedy i tylko wtedy) c) 3 rozwiązania będzie dla P = 9 oraz P = 10 −−−> a dla m=−3 mamy P = 9 + 1 = 10 d) więcej rozwiązań ujemnych niż dodatnich będzie dla P ∊ [9 , 10] co daje nam tutaj m ∊ [−3 ; −2√2] u [2√2 ; 3] a) jakiekolwiek rozwiązanie będzie dla P ≥ 1 −−−> dla m ∊ R

pati: Ślicznie Wam dziękuję