Układ 171: Mając np układ równań tego typu y = x²+2x y = x y = −x−2 Nie możemy podstawić np w ten sposób do (1) y = x*x+2x y = (y)²+2(−2−y) czyli jakby trochę z równania (2) a trochę z (3) albo np za x*x raz z tego raz tego itd Wtedy otrzymujemy rozwiązania dla y takie : {−1,4} Lecz skąd się bierze to 4? Bo faktycznie −1 jest rozwiązaniem tego potrójnego układu Przecież można również dobrze do tego dojść najpierw mnożąc *2 (2) i odejmując stronami a potem podstawiając (3) do (1 −2)

171: Czy jest jakaś reguła, że trzeba podstawiać tylko z jednego równania albo pominąłem jakieś założenie? Wiem że można to rozwiązać w pamięci... ale mam zagwostkę

. : Ten układ równań może mieć co najwyżej 1 rozwiązanie Zauważ że dwa z tych równań reprezentują proste. Proste (o ile nie mają takie samego współczynnika kierunkowego) przecinają się tylko w jednym miejscu.

chichi: liczba (4) jest rozwiązaniem równania y = y² + 2(2 − y), ale nie jest rozwiązaniem układu, bo wtedy: (2): x = 4, a (3): x = −6, zatem y = 4, zatem nie jest rozwiązaniem układu, natomiast dla y = −1 mamy: (2): x = −1 i tak samo (3): x = −1, stąd para (x,y) = (−1,−1) jest jedynym rozwiązaniem układu

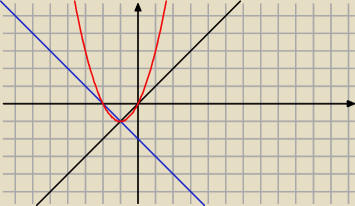
Fairy and Devil: Także jednym ze sposobów rozwiązywania układow równa jest sposób graficzny

171: Ta ja wiem że taki układ ma co najwyżej jedno rozwiązanie lecz po prostu mnie to zaciekawiło, że potem trzeba jak metodą starożytną sprawdzać rozwiązania jeśli ktoś by się wsadził w taki zaułek

171: Wiem że można rozwiązać i graficznie i macierze i UJ wie co xD

chichi: odejmowanie stronami na przykład nie jest równoważnym przekształceniem układu, jest jedynie implikacją w jedną stronę, zatem może wygenerować niechciane rozwiązania, stąd należy sprawdzić czy otrzymane rozwiązania są rzeczywiście poprawne

171: Aczkolwiek ciekawa rzecz że zawsze jedno z tych rozwiązań co nam wyjdzie będzie tym poprawnym

171: Dlaczego nie jest równoważnym przekształceniem?

171: Odejmowanie w tym przypadku można potraktować jako podstawienie jak napisałem wyżej

171: I w sumie podstawienie też może nie być równoważne prawda? Gdy podstawiamy np x = ... Za x² to teoretycznie potrzebne byłyby założenia czy nie ≥ 0

chichi: no np. dlatego iż prawdą jest, że jeśli a = b i c = d, to a + c = b + d, natomiast, nie jest na ogół prawdą, że jeżeli a + c = b + d, to a = b i c = d, więc powtórzę dodawanie równań stronami nie jest przekształceniem równoważnym ! ! !

171: A istnieje przekształcenie które jest? XD

chichi: oczywiście np. metoda podstawienia jest przekształceniem równoważnym układu

171: Jednak mimo to jak widać może generować niechciane rozwiązania

171: Dobra jakoś rozumiem mam nadzieję że ty również

chichi: no nie, po prostu nie rozumiesz co robisz

171: Ty chyba też nie do końca, pisząc że jest równoważne jak nie jest

171: Sam siebie zaprzeczyleś

171: Rozumiem i żartuję calm down dobranoc

chichi: twój układ ma więcej równań niż niewiadomych, a to odgrywa znaczącą rolę

171: Twierdzisz że w przypadku 3 niewiadomych i 3 równań nie byłoby tego problemu?

171: Teoretycznie jest taka możliwość

171: Ale tylko teoretycznie a w praktyce gadasz głupoty

171: Ahh Ci studenci UJ

171: Trochę dystansu