zadanie Liczby: Z papieru w kratke wycieto kwadrat o boku n kratek. Na ile sposobów mozna ten kwadrat podzielic na trzy prostokaty, wykonujac ciecia tylko po kratkach? Dla n=2 opisanego wyzej podziału mozna dokonac na 4 sposoby. a) Dla n=3 liczba sposobów podziału jest równa b) Dla n=4 liczba sposobów podziału jest równa c) Dla n=5 liczba sposobów podziału jest równa d) Dla n=6 liczba sposobów podziału jest równa

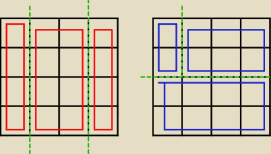
wredulus_pospolitus: 1) zauważ, że dla n > 2 mamy 4 różne typy podziałów (z czego mamy dwie pary analogicznych podziałów) I −−− dwa cięcia w pionie II −−− analogiczny do I −−− tylko tniemy w poziomie III −− jedno cięcie w poziomie i z pozostałej części jedno cięcie w pionie IV −−− analogicznie do III −−− tylko najpierw tniemy w pionie a następnie w jednej z części w poziomie Dzięki takiemu pogrupowaniu cięć, nie będziemy liczyć kilkukrotnie takich samych cięć (mimo że otrzymane prostokąty mogą się powielać). I teraz sprawdzamy ile jest możliwości cięć dla każdego z typu:

	n−1 2
I −−−−		(mamy n−1 linii w pionie, przez dwie z nich tniemy)

	n−1 2
II −−−		(analogicznie)

	n−1 1		n−1 1
III −−−		*2*		(mamy n−1 linii w poziomie, przez jedną z nich tniemy, następnie

wybieramy którą z części będziemy dalej ciąć, wybieramy linię w pionie i tniemy)

	n−1 1		n−1 1
IV −−−		*2*		(analogicznie)

dodajemy to do siebie, podstawiamy pod 'n' i mamy wyniki

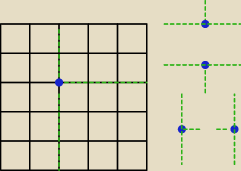
wredulus_pospolitus: Inne podejście do do tematu: I i II dokładnie tak samo. III i IV będzie zapisana jako jeden punkt −−− punkt wewnątrz wyjściowego kwadratu, który będzie wierzchołkiem dwóch prostokątów i leżał na boku trzeciego z nich..

n−1 1		n−1 1
	*		*4 −−−− wybieramy 'współrzędne' tegoż punktu, *4 możliwości podziału

(z boku rysunku zaprezentowałem możliwe podziały)

pa to l: @wredulus, gdybym ci mogl gonga zapodac w morde, zrobilbym to bez wahania

wredulus_pospolitus: to wpadaj do Gdańska