Sprawdź czy relacja jest przechodnia. hanka: Czy ta relacja jest przechodnia? R = {<a,a>, <b,b>, <c,c>, <a,b>}

ite: Czy relacja jest określona zbiorze {a, b, c} ?

hanka: tak, jest określona w zbiorze {a, b, c}

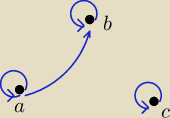
ite: relacja R spełnia warunek przechodniości

hanka: Dzięki za odpowiedź! Mogę prosić o jakieś wyjaśnienie dlaczego ta relacja jest przechodnia? Z moich informacji wynika, że relacja przechodnia to taka, że jeśli np. <a i b> i <b i c> są w relacji, to a musi być w relacji z c. Jednak w tym przykładzie mamy tylko 1 strzałkę (a−>b). Czy do przechodniości nie będą potrzebne 2 strzałki? I czy relacja przechodnia to taka która posiada tylko 1 taki "skrót" pomiędzy 2 łukami, czy pomiędzy każdymi dwoma łukami musi istnieć ten skrót?

ite: Relacja jest przechodnia, jeśli dla wszystkich par należących do tej relacji zachodzi zależność taka, że [(x, y)∊R ∧ (y, z)∊R] ⇒ (x,z)∊R Tutaj te "drogi" (nazwane o 21:57 "między łukami") wyglądają tak [(a, a)∊R ∧ (a, a)∊R] ⇒ (a, a)∊R [(a, a)∊R ∧ (a, b)∊R] ⇒ (a, b)∊R [(a, b)∊R ∧ (b, b)∊R] ⇒ (a, b)∊R [(c, c)∊R ∧ (c, c)∊R] ⇒ (c, c)∊R więc warunek przechodniości jest spełniony. Czy ten graf trochę wyjaśnił przechodniość?

ite: warunek: "dla wszystkich par należących do tej relacji" nie oznacza, że tylko z różnych par i z różnych elementów mamy budować (i sprawdzać te drogi) te 'drogi'

hanka: Dzięki wielkie, teraz rozumiem