okręgi Ausi: Niech O₁ i O₂ będą okręgami o tym samym środku i promieniach odpowiednio 9 cm i 15 cm. Niech A lezy na O₁ i B, C będą punktami na O₂ takimi, że odcinek BC jest styczny do O₁ i ∡ BAC = 90^o. Oblicz pole trójkąta ABC.

Ausi: Jak to rozwiązać?

a7: 1. zrobić rysunek

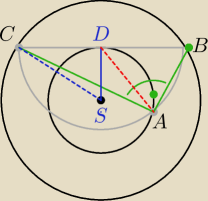
a7: z tw. Pitagorasa CD=12 CB=24 P=1/2|CB|*h=1/2|AB|*|AC| AB=DB=12 z tw. Pitagorasa AC=√24²−12²=12√3 P=1/2*12*12√3=72√3

a7: jeśli zbyt lakonicznie napisałam, to mogę wyjaśnić bardziej szczegółowo... nie wiem czy nie ma błędu(ów) obliczeniowych jakichś

a7: a chyba AB≠DB

kiwi: dzieki

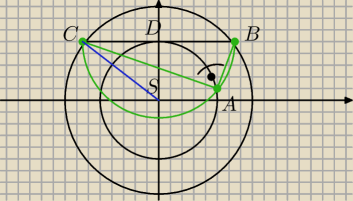
a7: y_B=9 x_B=12 81+x_B²=225 B=(12,9) C=(−12,9) S=(0,0) D=(0,9) DA=12 czyli |DA|=p{0−x_A)²+(3−√9−x_a²)² x_A=6√2 czyli y_A=3 x_A²+y_A²=81 x_A²=√81−y_A² y_A²=√81−x_A² BA=√(12−6√2)²+(9−3)²=√252−144√2 CA=√(−12−6√2)²+(9−3)²)=√252+144√2

	√252−144√2√252+144√2
PΔABC=1/2*|BA|*|CA|=		=18√17
	2

a7: |DA|=√(0−x_A)²+(9−√81−x_a²)²