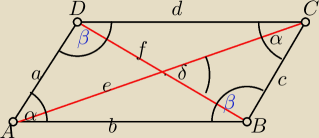
Podpunkt a sobie na luzie obliczyłem, wyszło 4 pierwiastki z dwóch, ale nie wych Mariusz : W równoległoboku ABCD bok AB ma długość 4, zaś bok BC ma długość 2. Kąt BAD jest równy 45°. Oblicz: a) pole równoległoboku b) sinus kąta przecięcia przekątnych

X:

Little Mint: W równoległoboku a=c=2 oraz b=d=4 ∡BAD=∡BCD=45^o ∡ADC=∡ABC=135^o e i f to przekatne tego rownoległoboku δ− kąt miedzy przekątnymi tego rownoległoboku Kąt δ miedzy przekątnymi tego równoległoboku obliczymy ze wzoru

	1
S=		e*f*sinδ
	2

S mamy juz policzone Długości przekątnych policzyc z twierdzenia cosinusów można lub skorzystać ze wzoru dla czworokata wypukłego e²*f²=a²*c²+b²*d²−2*a*b*c*d* cos2ω gdzie cos2ω=∡BAD+∡DCB lub ∡ADC+∡ABC

Little Mint: Musze poprawic gdzie 2ω= i te kąty a nie cos2ω

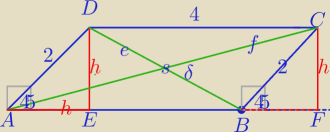Mila: 1) P_ABCD=4*2*sin45^o=4√2 w ΔAED: h=√2 2)

1		1		1
	*		*e*		f sinδ=√2
2		2		2

e*f sinδ=8√2 3) W ΔDEB: e²=(4−√2)²+(√2)² e²=20−8√2 W ΔAFC: f²=(4+√2)²+√2² f²=20+8√2 4) e²*f²=(20−8√2)*(20+8√2)=400−64*2=272 e*f=√272 Podstawiając do(2): √272*sinδ=8√2

	8		8		4
sinδ=		=		=
	√136		2√34		√34

Sprawdzaj rachunki Może ładniejszy wynik dostaniesz.

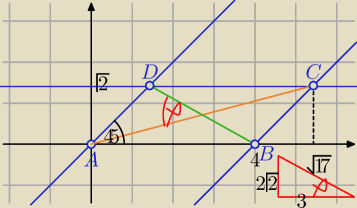Eta: 2 sposób ( z zastosowaniem narzędzi geometrii analitcznej ) Umieszczam równoległobok w układzie kartezjańskim A=(0,0) , B=(4,0) , C=(√2+4, √2) , D=(√2, √2) bo proste mają równania AD : y=x i BC : y=x−4 kąt φ między przekątnymi AC i BD

	a1−a2
tgφ= |		| gdzie a1, a2 współczynniki kierunkowe prostych AC i BD
	1+a1*a2

	√2		√2
a1=		, a2=
	√2+4		√2−4

................................... teraz "kosmetyka" obliczeń i otrzymujemy

	−8√2		2√2
tgφ=|		|=
	−12		3

	2√2		4
to sinφ=		=		−− jak u Mili
	√17		√34

Mila:

Aa: 10 1024 9