Trójkąty, poziom rozszerzony, kąty. Patrycja: W kątach przyległych ABC, DBC poprowadzono dwusieczne i prostą, równoległą do AD, która przecina te dwusieczne odpowiednio w punktach E i F, zaś ramię BC przecina w punkcie K. Wykaż, że |EK|=|KF|. Doszłam do tego, że poprowadziłam symetralną prostopadle do prostych równoległych i zorientowałam sie, że po przedłużeniu dwusiecznych zetkną się w miejscu który powinien utworzyć trójkąt równoramienny i żeby udowodnić równość |EK|=|KF| trzeba udowodnić równość kątów przy podstawie w tym trójkącie. Niestety nie wiem jak to dalej pociągnąć..

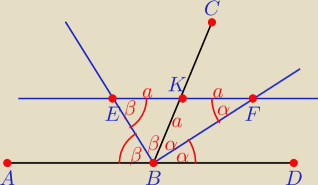
frykas: Podpowiedź: kąty ABE i BEK oraz DBF i BFK to kąty naprzemianległe.

Patrycja: dziekuję! faktycznie