kwadraty
dydo:
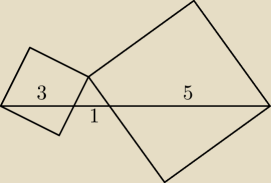
Oblicz ile wynosi suma pol powyższych kwadratów?
15 maj 23:49
a7: a skad to zadanie?
\
16 maj 20:03
Kacper: Może jakiś konkurs.
16 maj 21:19
dydo: Tak to zadanie z jakiegoś dawnego konkursu, wiec trudniejsze
17 maj 14:30
chichi:
ono nie jest trudne, tylko rysunek wymaga trochę pracy i dorobienia czegoś, próbowałeś coś?

17 maj 15:02
dydo: Niestety nie mam pomysłu
17 maj 15:56
Kacper: Ja zrobiłem w układzie współrzędnych, ale zapewne istnieją lepsze pomysły 😁
17 maj 17:34
dydo: Możesz zatem pokazać

17 maj 17:48
dody: *
17 maj 17:48
Mila:
Jakie masz pole Kacper?
17 maj 20:04
Kacper: Zaraz sprawdzę, bo robiłem rysunek w geogebrze.
17 maj 20:25
kkk:
Za pomocą cyrkla można sprawdzić, że trójkąt między kwadratami jest równoboczny o długości boku
1.
Stąd łatwo sprawdzić, że długość boku mniejszego kwadratu równa jest 2 a większego 4. Pole=20.
17 maj 20:31
Kacper: Wyszło mi 212126 dziwnie trochę, ale muszę sprawdzić czy błędu nie mam.
17 maj 20:38
kkk:
@Kacper
Twój wynik jest zapewne bardziej zbliżony do wyniku rzeczywistego. Sądzę, że jest to zadanie na
umiejętność posługiwania się cyrklem dla uczniów szkoły podstawowej.
17 maj 20:47
Kacper: Zależy wszystko od tego na jakim poziomie to zadanie.
Ja obstawiam, że to poziom liceum i chcą dokładny wynik.
Chichi może wynik podaj jaki otrzymałeś?
17 maj 21:01
chichi:
@
Kacper w wolnej chwili zrobię i podam wynik, nie przeliczałem konkretnie tego zadania,
ale robiłem w przeszłości z dzieciakami podobne zadanka

17 maj 21:11
Kacper: Interesuje mnie w sumie jak wyznaczyć ten punkt wspólny kwadratów bez geometrii analitycznej.
Ja jakoś pomysłu nie mam.
17 maj 21:14
.: A w geometrii analitycznej jak wyznaczyłeś?
17 maj 23:19
.: Ja mam pomysł z kątami
17 maj 23:30
.:
@Kacper −−− chcialbym zauważyć, że jeżeli by tenże trojkąt był trójkątem równobocznym, to mały
kwadrat nie miałby boku długości '2' tylko:
| | √17−1 | |
9 = (x+1)2 + x2 −−−> 2x2 + 2x − 8 = 0 −−−> x2 + x − 4 = 0 −−−> x = |
| |
| | 2 | |
(bo oczywiście x>0)
| | 1+√17 | |
−−−> długość boku kwadratu równa jest x+1 = |
| |
| | 2 | |
18 maj 00:18
Kacper: Wyznaczyłem równania okręgów po których poruszają się wierzchołki kwadratów, które się przetną.
Potem wyznaczyłem punkt ich przecięcia i dalej to już prosto.
18 maj 07:40
123: | | 3 | |
Ale znów traktując trójkąt jako 30,60,90... wychodzi bok |
| √3 ≈ 2,59 a wynik z 00:18 to ≈ |
| | 2 | |
2,56
18 maj 09:56
123: Wychodzi rozbieżność α ≈ 58°,
Kacper pokazalbys jak wyznaczyć równania okręgów?
18 maj 10:08
123: Jedyny wniosek jaki się nasuwa to, że odcinek "1" łączący kwadraty nie jest współliniowy stąd α
≠ 60
18 maj 10:15
123: Chyba dobrze mówię

a odnośnie geogebry nigdy się tak nie bawiłem, a pewnie jest możliwość że
sama poda równanie...
18 maj 10:24
123: Głupoty napisałem, wtedy jeden bok będzie 2,56 drugi 2,5...

18 maj 10:34
123: Czyli nie jest równoboczny, ale monolog prowadzę
18 maj 10:45
x: 567/26
18 maj 16:57
Kacper: Mila liczyłaś może to zadanko?
18 maj 17:40
.: Chichi chyba ma problem z rozwiązaniem

19 maj 07:24
123: Chyba tak


19 maj 21:00
123: Chyba jeszcze rysunek tworzy

19 maj 21:00
a7: Obliczyłam chyba

19 maj 23:07
a7: a+b2=14,875
19 maj 23:10
Ptyś:
skąd ten wynik?
19 maj 23:12
x: wynik to 567/26
19 maj 23:15
123: Niestety, ale niekiedy są ludzie, którzy czerpią radość z trollowania i podszywania się.
19 maj 23:33
a7: oznaczenia
a−bok kwadratu z trójką
b− bok kwadratu z piątką
h wysokość trójkąta
x,y boki trójkąta
α−górny kąt trójkąta
1.z tw cosinusów
9
2=(a
√2)
2+(b
√2)
2−2a
√2*b
√2*cos(90+α)
2.z podobieństwa trójkątów h/a=3/x oraz h/b=5/y oraz 1/2*xysinα=h (pole trójkącika wyrażone
na dwa sposoby)
3.czyli a
2+b
2=40,5−4/15*h
3 *)
4.z twierdzenia cosinusów
9=x
2+(ap[2})
2−2a
√2x*
√2/2 oraz
25=y
2+(b
√2)
2−2b
√2y
√2/2
odejmujemy stronami
16=y
2−x
2+2b−2a+2ax−2by oraz dodajemy stronami
34=y
2+x
2+2a
2+2b
2−2ax−2by
____________________________
50=2y
22a
2+2b
2+2b−2a−4by |:2
25=y
2+a
2+b
2+b−a−2by
przekształcamy
25=(b−y)
2+a
2+a
z tw Pitagorasa (b−y)
2+b
2=25 czyli (b−y)
2=25−b
2
podstawiamy
25=25−b
2+a
2+a
b
2=a
2−a
z*) mamy a
2+b
2=40,5+4/15*h
3
czyli a
2+a
2−a=..... czyli
a
2+a
2−a=40,5+4/15*h
3 stąd h
3=2a
2−a−40,5)*15/4
następnie
jeszcze raz *) czyli a
2+b
2=40,5 − 4/15*h
3
podstawiamy
a
2+a
2−a=40,5−4/15*15/4(2a
2−a−10,5)
stąd
4a
2−2a+81=0
| | 1+√82 | | 79−2√82 | |
a= |
| czyli b= |
| |
| | 4 | | 16 | |
| | 284√82+7897 | |
a2+b2= |
| ≈40,893474.... |
| | 256 | |
19 maj 23:49
a7: @Mila lub @Eta i wszyscy inny czy można prosić o weryfikację?
19 maj 23:51
a7: no jeszcze poprawiam chochliki
4a2−2a−81=0
20 maj 00:06
an: wynik końcowy a7 jest błędny już na pierwszy rzut oka gdyż a<3 ;b<5 to a
2+b
2<34
| 162+405 | | 567 | |
| = |
| jest prawidłowy lub z bardzo dużą dokładnością |
| 26 | | 26 | |
20 maj 09:52
wredulus_pospolitus:
w (2)
pole trójkąta na dwa sposoby:
20 maj 15:16
123: W pewnym momencie w "z*)" oraz "*)" zamieniłeś znak z − na + po 40,5
Wyznaczyleś coś z jednego równania i do tego samego tak naprawdę podstawiłeś, wyszła by
tożsamość a przez tą nieuwagę
niby mamy jakieś rozwiązanie jak mi się wydaje
20 maj 20:27
123: Poza tym wszystko git, ale brakuje chyba jeszcze czegoś
20 maj 20:27
20 maj 20:36
kiwi:
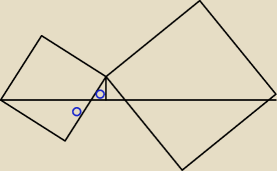
Skorzystałem z podobieństwa tych trójkątów
20 maj 21:29
Kacper: Czyli mój sposób w sumie łatwiejszy rachunkowo 😏
21 maj 19:55
a7: No u mnie ileś błędów. Nie tylko rachunkowych….
21 maj 21:32
Mila:
Chcę uniknąć tych obłędnych rachunków.
Szukam wszystkich własności tej konstrukcji, kilka odkryłam, ale to nie przybliżyło mnie
do rozwiązania geometrycznego.
Pozdrawiam wszystkich pasjonatów
 a7
a7, popatrzyłam na Twoje rachunki, postaram się dokładnie prześledzić.

21 maj 22:07
a7: zrobiłam na pewno błąd w podobieństwie trójkątów nietą przyprostokątną wzięłam i odwrotna
proporcja mi się zrobiła oraz właśnie błąd przy podwójnym wyrażeniu pola trójkąta też źle,
także chyba całość jest źle
21 maj 22:10
a7: ponadto w jednym z tw cosinusów nie podniosła a i b do kwadratu i raz pominęłam b stad wszytsko
jest na pewno obarczone poważnymi blędami
21 maj 22:13
Mila:
Błędy rachunkowe można poprawić, na razie zostaw problem, jak się odleży, to rozwiążemy.

21 maj 23:41
a7: 
22 maj 00:49
Kacper: Miła ja dopiero wpadłem jak analitycznie to zrobić jak sobie zrobiłem symulacje w
geogebrze.
22 maj 07:46
kiwi:
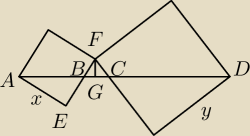
BE=
√9−x2
BF=x−
√9−x2
ABE∼BFG
| | BE * BF | | x√9−x2−9+x2 | |
BG= |
| = |
| |
| | 3 | | 3 | |
| | x * BF | | x2−x√9−x2 | |
FG= |
| = |
| |
| | 3 | | 3 | |
Podobnie z większym kwadratem
Zatem
| x√9−x2−9+x2 | | y√25−y2−25+y2 | |
| + |
| =1 |
| 3 | | 5 | |
| x2−x√9−x2 | | y2−y√25−y2 | |
| = |
| |
| 3 | | 5 | |
x=? y=?
22 maj 12:05
. :
Wiec jednak tak jak wtedy pisałem − miałeś błąd w drugim równaniu

22 maj 13:21
kiwi: Tak, ale nie wiem jak rozwiązać ten układ

22 maj 15:42
a7: a do wolframa się nie da go wprowadzić?
22 maj 15:52
22 maj 16:01
22 maj 16:08
a7: w linku 16:08 poprawka
22 maj 16:08
kiwi: To jednak trzeba inaczej rozwiązać zadanie
22 maj 16:10
a7: Wynik z wolframa zgadza się z wynikiem Kacpra
22 maj 19:34
a7: Także ten układ @kiwi jest pewnie do rozwiązania i na piechotę
22 maj 19:42
123: To samo pisałem, drugie równanie miało "literówkę" a układ może rozwiązać w przybliżeniu jak i
na pewno dokładny wynik lecz trzeba się bawić w wolframowe
22 maj 19:46
a7: pierwsze równanie razy 15
5x
√9−x2−45+5x
2+3y
√25−y2−75+3y
2=15
5x
√9−x2+5x
2+3y
√25−y2+3y
2=135
drugie równanie też razy 15
5x
2−5x
√9−x2=3y
2−3y
√25−y2
5x
2=3y
2−3y
√25−y2+5x
√9−x2
wstawiamy do pierwszego 5x
2
3y
2−3y
√25−y2+5x
√9−x2+5x
√9−x2+3y
√25−y2+3y
2=135
czyli 6y
2+10x
√9−x2=135
czyli 10x
√9−x2=135−6y
2
podnosimy obie strony do kwadratu
100x
2(9−x
2)=135
2−2*135*6y
2+36y
4
czyli mamy
900x
2−100x
4=135
2−1620y
2+36y
4 *)
z pierwszego (pomnożonego przez 15) wyznaczamy 5x
√9−x2 wstawiamy do drugiego (pomnożonego
przez 15)
po redukcji zostaje 6y
√25−y2=135−10x
2
podnosimy do kwadratu i mamy
36y
2(25−y
2)=135
2−2*135*10x
2+100x
4
900y
2−36y
4=135
2−2*135*10x
2+100x
4
teraz bierzemy *)
900x
2−100x
4=135
2−1620y
2+36y
4
900y
2−36y
4=135
2−2*135*10x
2+100x
4
odejmujemy stronami
900x
2−900y
2−100x
4+36y
4=135
2−135
2−1620y
2+20*135*x
2+36y
4−100x
4
900x
2−2700x
2−900y
2+1620y
2=0
720y
2−1800x
2=0
2y
2−5x
2=0
i teraz się zgadza
podstawiamy
do 6y
√25−y2=135−10x
2
wychodzi
po podniesieniu do kwadratu
36*5/2x
2(25−5/2x
2)=135
2−2700x
2−100x
4
noi podstawiamy t
i mamy x=3 x=9/
√13

23 maj 18:44
a7: oczywiście +100
4
czyli
2250x
2−225x
4=135
2−2700x
2+100x
4
13t
2−198t+729=0
Δ=39204−4*13*729=1296
√Δ=36
| | 198−36 | | 81 | | 198+36 | |
t1= |
| = |
| lub t2= |
| =9 |
| | 26 | | 13 | | 26 | |
| | 9 | |
x>0 czyli x= |
| lub x=3 |
| | √13 | |

23 maj 19:07
Mila:
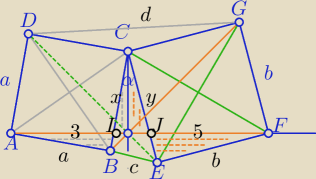
1)
| ax | | 3 | |
| = |
| ⇔ 5ax=3by z podobieństwa Δ |
| by | | 5 | |
Stosunek pól: ΔAJC i ΔCIF:
| a√2*y*sin(α+45) | | 2 | |
| = |
| ⇔ |
| x*b√2*sin(α+45) | | 3 | |
===============
5a
2=2b
2
==============
2) Związek między x i y:
2bx=3ay /
2
4b
2x
2=9a
2y
2
10a
2*x
2=9a
2y
2
=========
3)ΔJEF i ΔABI
(b−y)
2+b
2=25
| | √2 | | 3y | | 2 | |
(b |
| − |
| )2+ |
| b2=9 |
| | √5 | | √10 | | 5 | |
23 maj 23:59
a7: 
24 maj 07:44
a7: To czyli są już trzy sposoby na rozwiązanie…
24 maj 07:59
Mila:
A7
Układ tak samo skomplikowany jak u poprzedników.
Rezygnuję z punktu (3), było późno i nie rozwiązywałam tego układu.
Dalej poszukam prostych obliczeń.

24 maj 15:49
Kacper: Może Eta ma jakiś pomysł, gdzie rozwiązanie robi się w 2 linijkach. Na pewno takie
istnieje 😁
24 maj 15:53
a7: mi się wydaje, że układ Mili jest prostszy niż pozostałe, i wątpię, żeby się dało w dwóch
linijkach,
ale Eta chyba na urlopie, bo jeszcze nie zabrała głosu?
24 maj 16:29
a7: prostszy w sensie do obliczeń , ale dla bardzo spostrzegawczych i trudno na niego wpaść
24 maj 16:32
kaszojadka: czy możliwe, że wynik to 20,5?
jeżeli możliwe to przeliczę jeszcze raz
24 maj 17:06
a7: | | 21 | |
Wynik podał chyba jako pierwszy Kacper 21 |
| |
| | 26 | |
24 maj 17:12
kaszojadka: gdyby narysować coś takiego, że tam gdzie są początki tych odcinków (na wierzchołkach
kwadratów) dorysować coś wokół tych punktów tak, żeby wyszedł czworokąt i żeby na tym
czworokącie opisać okrąg, którego środkiem będzie właśnie ten wierzchołek z którego wychodzi
ten odcinek
i na drugim kwadracie coś podobnego
odległość między środkami okręgów będzie 9, czyli suma promieni będzie 9, czyli suma
przekątnych kwadratów będzie 9
i wziąć to 9 podzielić np., że jeden kwadrat ma przekątną 4, a drugi 5 (jakieś losowe liczby),
więc jeden ma bok 2
√2, a drugi 2,5
√2,
wtedy jeden ma pole 8, a drugi 12,5
razem ich pola mają 20,5
tylko nie wiem czy te okręgi nie będą na siebie nachodzić, a wtedy to nie zadziała... Trzeba
wykombinować, żeby się stykały, ale nie nachodziły

24 maj 17:18
kiwi: W analitycznej geometrii też wychodzi chyba też dość trudny układ
24 maj 17:30
kaszojadka: @Mila
24 maj 19:04
Kacper: W analitycznej należy znaleźć punkty wspólne dwóch okręgów, rachunkowo to proste. Jeden z tych
punktów to wspólny wierzchołek kwadratów.
24 maj 20:15
Mila:
Kacper zauważyłeś, że ta konstrukcja ma bardzo dużo ciekawych własności.
Polecam wpisać
1) Twierdzenie Bottemy − dowód bez słów.
oraz
2) Triangle and two squares − przeglądaj rysunki − pojawią się tw. dotyczące tej konstrukcji.
15 cze 21:52
a7: u mnie nie ma wyników dla "Twierdzenie Bottemy"

18 cze 13:32
Kacper: wpisz theorem bottema's
18 cze 15:30
a7: Dziękuję, jest

18 cze 16:49
Mila:
a7 Podobały się materiały?
Przeczytałaś wszystko z Bottemy? Tłumaczenie jest okropne, ale jeśli ktoś zna angielski
to dużo skorzysta.
24 cze 15:12
a7: to znaczy, ja zajrzałam tylko, jako ciekawostkę, nie studiowałam wnikliwie, ale dzięki za fajną
ciekawostkę

26 cze 20:37
Mila:
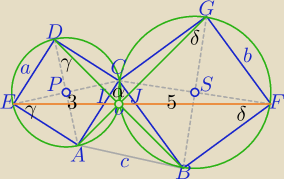
0<a<3, 0<b<5
|IJ|=1, |EI|=3, |FJ|=5
1) ΔDCB≡ΔBCG : a ,90+α,b
Δ te są podobne do ΔEFC, a
√2,90+α, b
√2
| | a | | |DO| | | a2√2 | |
2) ΔAIE∼ΔAOD⇔ |
| = |
| ⇔|DO|= |
| |
| | 3 | | a√2 | | 3 | |
| | 2 | | a2√2 | |
3)a2= |
| b2 ( 23:59)⇒|GO|= |
| |
| | 5 | | 2 | |
| | 9√2 | | a2√2 | | √2 | |
4) |AO|= |
| − |
| = |
| (9−a2) |
| | 2 | | 2 | | 2 | |
5) W ΔAOD:
| | √2 | | a2√2 | |
(a√2)2=( |
| (9−a2))2+( |
| )2⇔ |
| | 2 | | 3 | |
Δ=4
| | 11−2 | | 81 | |
a2= |
| = |
| lub a2=9∉D |
| | | | 13 | |
=====================
20 lip 20:17
kalkulator: problem się odleżał 2 lata i został rozwiązany

21 lip 09:43
 Oblicz ile wynosi suma pol powyższych kwadratów?
Oblicz ile wynosi suma pol powyższych kwadratów?



 a odnośnie geogebry nigdy się tak nie bawiłem, a pewnie jest możliwość że
sama poda równanie...
a odnośnie geogebry nigdy się tak nie bawiłem, a pewnie jest możliwość że
sama poda równanie...






 Skorzystałem z podobieństwa tych trójkątów
Skorzystałem z podobieństwa tych trójkątów
 a7, popatrzyłam na Twoje rachunki, postaram się dokładnie prześledzić.
a7, popatrzyłam na Twoje rachunki, postaram się dokładnie prześledzić.


 BE=√9−x2
BF=x−√9−x2
ABE∼BFG
BE=√9−x2
BF=x−√9−x2
ABE∼BFG




 1)
1)






 0<a<3, 0<b<5
|IJ|=1, |EI|=3, |FJ|=5
1) ΔDCB≡ΔBCG : a ,90+α,b
Δ te są podobne do ΔEFC, a√2,90+α, b√2
0<a<3, 0<b<5
|IJ|=1, |EI|=3, |FJ|=5
1) ΔDCB≡ΔBCG : a ,90+α,b
Δ te są podobne do ΔEFC, a√2,90+α, b√2
