trygonometria tom: (2sinx −3)(2sinx +1 ) > 0 w przedziale (0 ; 2pi)

. : I w czym problem

frykas:

	1
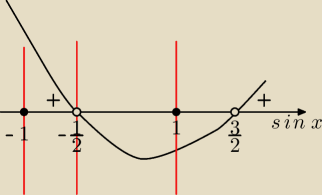
−1 ≤ sin(x) < −		dla x ∊ (0, 2π)
	2

tom: i moze ktos wytlumaczyc to rozwiazanie? Bo nie rozumiem za bardzo. iloczyn ma byc dodatni czyli oba maja byc ujemne albo oba dodatnie?

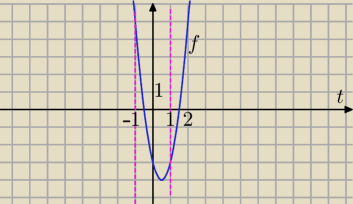Mila: (1) sinx=t, −1≤t≤1 f(t)=(2t−3)(2t+1) (2t−3)(2t+1)>0

	3		1
(t−		)*(t+		)>0 i −1≤t≤1
	2		2

	1		3
[t<−		lub t>		) ] i −1≤t≤1⇔
	2		2

	−1
t∊<−1,		)
	2

	1
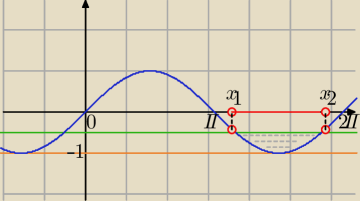
−1≤sinx<−		i x∊(0,2π)
	2

cdn

Mila:

	1
sin(x)=−
	2

	π		π
x=π+		lub x=2π−
	6		6

	7π		11π
x1=		lub x2=
	6		6

	7π		11π
x∊(		,		)
	6		6