 Cześć, czy wysokość opuszczona na podstawę trójkątka równoramiennego zawsze jest równa połowie
podstawy czy tylko po wpisaniu w okrąg?
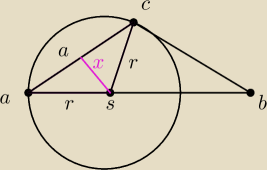
Mam takie zadanie: Wierzchołki a i c trójkąta abc leżą na okręgu o promieniu r, a środek S tego
okręgu leży na boku ab trójkąta. Prosta bc jest styczna do tego okręgu w punkcie c, a ponadto
|ac|= r √3 Wykaż, że kąt ACB ma miarę 120°
Cześć, czy wysokość opuszczona na podstawę trójkątka równoramiennego zawsze jest równa połowie
podstawy czy tylko po wpisaniu w okrąg?
Mam takie zadanie: Wierzchołki a i c trójkąta abc leżą na okręgu o promieniu r, a środek S tego
okręgu leży na boku ab trójkąta. Prosta bc jest styczna do tego okręgu w punkcie c, a ponadto
|ac|= r √3 Wykaż, że kąt ACB ma miarę 120°
| r √3 | ||
Czy na moim rysunku x= | ? | |
| 2 |

| 1 | x | |||
sin(30o) = | = | − − − > x = r/2 | ||
| 2 | r |

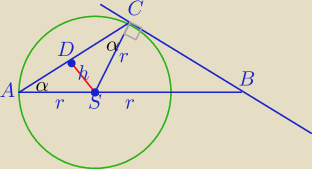 |AC|=r√3
|AC|=r√3
| r√3 | ||
|AD|=|DC|= | ||
| 2 |
| r√3 | r | |||
h2=r2−( | )2 ⇔h= | |||
| 2 | 2 |
| r/2 | 1 | |||
sinα= | = | , α− kąt ostry | ||
| r | 2 |