Zadanie Ziemia: https://ibb.co/vZhDRTB Co tu jest zle

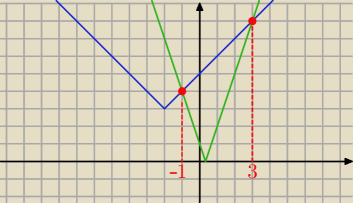
Niebo: graficznie: |3x−1|=|x+2|+3 y= |3x−1| i y= |x+2| Odp : x= −1 v x= 3 =============

Niebo: algebraicznie x∊(−∞, −2) | x∊<−2,1/3) | x∊<1/3,∞) =========================================================== −3x+1+x+2=3 | −3x+1−x−2=3 | 3x−1−x−2=3 x=0 x= −1 x= 3 nie jest rozw. jest rozw. jest rozw. Odp: x= −1 v x= 3 ============

asw: tak ale co w moim zapisie jest nie tak ze te rozwiazania mi odpadaja w tych przedzialach?

Niebo: Czy teraz już widzisz swoje błędy ?

asw: wlasnie nie

asw: nie wiem czemu tak skoro jest przedzial (−∞ ; − 2) no to I1−3xI jest na lewo wiec daje minusy a Ix+2I tez na lewo wiec daje minusy i wychodzi 3x−1 +x +2 =3

Niebo: √1+9x²−6x=√(3x−1)²= |3x−1| bo |1−3x|=|3x−1| √x²+4x+4=√(x+2)²=|x+2|

asw: a czemu to jest blad? Robiac ta metoda musze awazac w jakiej kolejnosci dam te cyfry?

Ted: Popełniłeś błąd w momencie, gdy po lewej stronie ¹₃ napisałeś 3x−1, a po prawej 1−3x. Powinieneś napisać odwrotnie. Jaki znak 1−3x jest po lewej stronie ¹₃ ustalasz biorąc jakąś liczbę mniejszą od ¹₃. Przykładowo x=0 < ¹₃, więc dla x=0 mam 1−3x = 1−3*0 = 1−0=1 > 0, więc po lewej stronie liczby ¹₃ nie zmieniam znaku i piszę 1−3x. Dla x=1>¹₃ mam 1−3x=1−3*1 = 1−3 = −2 < 0, więc po prawej stronie liczby ¹₃ zmieniam znak i piszę −(1−3x) = 3x−1. Z x+2 już nie ma takich problemów i napisałeś dobrze.