iwo trójkąt: W trójkącie ABC punkt D jest środkiem odcinka AB. Bok BC podzielano na trzy równe części. Niech E bedzie jednym z punktów tego podziału bliżej C. Wiedząc że ∡.ADC = ∡BAE, wyznacz kąt BAC.

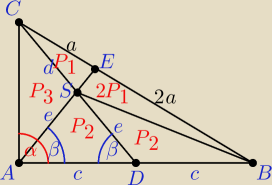
Bogdan: P₁, P₂, P₃ − pola trójkątów 2P₁ + 2P₃ = 2P₁ + 2P₂ ⇒ P₂ = P₃, zatem f = e e = |DS| = |AS| = |CS|, S jest środkiem okręgu opisanego na trójkącie ADC i S leży na środku CD, wobec tego trójkąt ADC jest prostokątny, kąt BAC jest prosty.

Bogdan: zatem d = e (nie f)

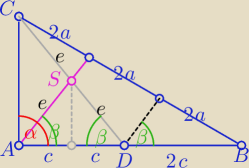
kąt: S środek okręgu opisanego na trójkącie ADC o promieniu długości : e=R to Δ ADC prostokątny α=90^o