szescian
Tymek: Niech A B C D A' B' C' D' będzie sześcianem o krawędzi 1. Na krawędzi BC leży punkt J taki ze
3|CJ| = |BC|, na krawędzi A' D' znajduje się punkt M taki ze 3 |A'M| = |A' D'|. Oblicz pole
trójkąta MDJ.
3 maj 14:55
enter:
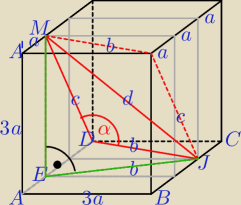
| | 1 | |
a = |
| , |AB| = |BC| = 3a, |JC| = |A' M| = a, |BJ| = 2a |
| | 3 | |
Kilka razy Pitagorasy, cosα z twierdzenia cosinusów, sinα z jedynki trygonometrycznej,
3 maj 17:11
Mila:
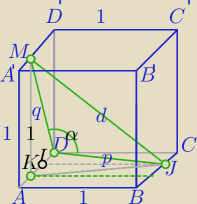
1)
|IJ|=1
|KJ|=p
2)
d
2=p
2+q
2−2*p*q cosα
dokończ rachunki
3 maj 17:26

 1)
1)