zbadaj liczbę rozwiązań układu równań w zależności od parametru m Jędrzej: Dzień dobry poproszę o pomoc w rozwiązaniu tego zadania. po narysowaniu hiperboli yx=2 i prostej y=x−1, chciałem za pomocą prostej y=mx na piechotę ustalić liczbę rozwiązań, jednak moje wyniki nie zgadzają się z odpowiedziami w książce, niestety nie wiem gdzie popełniam błąd x*y=2 ∧ (y−x+1)(y−mx)=0

wredulus_pospolitus: Wybacz, ale czy możesz jaśniej wyjaśnić co masz zrobić w zadaniu i co dokładnie zrobiłeś

ABC: napisz wyjściowy układ równań

Jędrzej: przepraszam za niejasności, napisałem pierwszy post i wyszło chaotycznie. Treść zadania: Zbadaj liczbę rozwiązań układu równań w zależności od parametru m. układ równań: x*y=2 ⋀ (x−y+1)(y−mx)=0

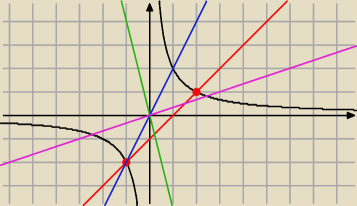
wredulus_pospolitus: mamy dwa rozwiązania z prostej: y = x−1 czerwona prosta y = mx dorzuci nam: 1) 0 rozwiązań jeżeli m< 0 zielona 2) 1 rozwiązanie jeżeli m= 0.5 lub m = 2 (jedno rozwiązanie będzie wspólne z y=x−1) niebieska 3) 2 rozwiązania dla m > 0 i m ≠ 0.5 i m ≠ 2 fioletowa

Jędrzej: Ach, no tak, chodzi o to, że sumujemy punkty wspólne prostych i hiperboli, ale nie punkty wspólne samych prostych. Dzięki, niby jasne, ale czasem potrzebna jest pomocna dłoń. miłego wieczoru