czworokat liceum: Przekątna AB w czworokąt ADBC dzieli kąt CBD na pół, DB i DA są styczne do okręgu opisanego na trójkącie ABC odpowiednio w punktach B i A. Jeśli obwód trójkąta ABC wynosi 20, a obwód trójkąta ABD również wynosi 20, jaka jest długość BD? Jak to zrobić?

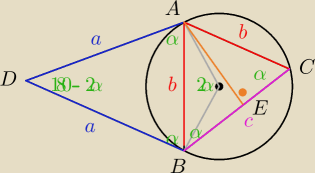
Saizou : b = 20−2a c = 4a−20 Z tw. cosinusów w ABD mamy (20−2a)² = a²+a²−2a*a*cos(180−2α) ... (20−2a)² = (2acosα)²

	2a−10
W trójkącie AEC mamy cosα =		, zatem
	20−2a

	2a−10
(20−2a)2 = (2a*		)
	20−2a

....

	20
a =
	3

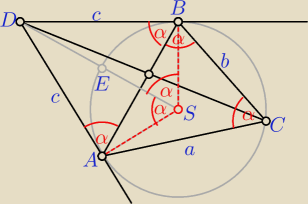enter: albo tak: |AD| = |BD| = c, |AC| = a|, |BC| = b, |AB| = d Kąty DAB i DBA (między cięciwą i styczną) to kąty dopisane, kąt ACB to kąt wpisany oparty o łuk AEB, wszystkie te kąty mają równe miary. Trójkąt ABC jest równoramienny: a = d. 2a + b = 20 ⇒ b = 2(10 − a)

	20 − a
a + 2c = 20 ⇒ c =
	2

a		c
	=		⇒ a2 = bc ponieważ trójkąty ABD i ABC są podobne.
b		a

	2(10 − a)(20 − a)		20
a2 =		⇒ a2 = 200 − 30a + a2 ⇒ 30a = 200 ⇒ a =
	2		3

	20
oraz b = c = a =		, trójkąty ABC i ABD są równoboczne i przystające.
	3

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Można najpierw spróbować wykazać, że te trójkąty są przystające, bo jeśli są przystające, to biorąc pod uwagę ich podobieństwo i równość obwodów otrzymamy: a = b = c

	20
i wtedy 3a = 20 ⇒ a =
	3