Optymalizacja Milena: Do wyznaczenia trzech pastwisk na pewnej ła˛ce nalez˙y uz˙yc´ ogrodzenia elektrycznego o ła˛cznej długos´ci 960 metrów. Dwa z tych pastwisk maja˛miec´ kwadratowy kształt, a trzecie mamiec´ kształt prostoka˛ta, którego jeden z boków jest dwa razy dłuz˙ szy od boku pastwiska w kształcie kwadratu

an: Czyli mamy dwa kwadraty o boku x i prostokąt o boku 2x pozostałe boki prostokąta z reszty drutu, to suma powierzchni wyniesie?

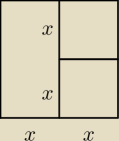
.: żeby nie było wymówek −− rysunek załączony

an: Jeden z boków prostokąta >>którego jeden z boków jest dwa razy dłuz˙ szy od boku pastwiska w kształcie kwadratu<< na rysunku drugi bok prostokąta jest x, a to nieprawda, nie mówiąc o tym że nie ma tu właściwie czego liczyć jest kwadrat o boku 2x

kerajs: Ciekawe dlaczego autor wybrał liczbę 960, która dzieli się przez 12, ale nie przez 11 ? PS Urzeka mnie niefrasobliwość autorów niektórych zadań z kontekstem realistycznym. Akurat w tym zadaniu intryguje mnie czy autor ma jakiekolwiek pojęcie o dzieleniu na części i zasilaniu ww. ogrodzenia.

an: Do czego podzielność przez 11 P=2x²+2x(960−9x)

	960
xmax=
	16

co do funkcjonalności to powinien się wypowiedzieć rolnik choć chyba nie można powiedzieć, że taki podział w konkretnej sytuacji nie może być potrzebny. Z elektrycznością jestem związany zawodowo i nie widzę problemów z zasilaniem, choć ze względu na ułatwienie lokalizacji ewentualnych doziemień należałoby to zrobić w układzie gwiaździstym i tu pole do popisu "optymalizacji" jak to zaprojektować, aby najmniej się nachodzić.

kerajs: No wreszcie! W końcu zauważono, że rysunek jest błędny a treść niepełna.