funkcja wymierna silnia:

x+|x+2|
	≥1 D=R\{−1}
x+1

Tego typu nierówności najlepiej rozwiązywać przedziałami, tj. I) x∊(−∞,−2)

x−x−2|
	≥1
x+1

−2
	≥1
x+1

−2		x+1
	−		≥0
x+1		x+1

(−x−3)(x+1)≥0 x∊<−3,1) II) x∊<2, +∞)

x+x+2
	≥1
x+1

2x+2		x+1
	−		≥0
x+1		x+1

(x+1)(x+1)≥0 x∊(−∞,−1)∪(−1,+∞) Cos niby swita jak z kluczem, ale te przedzialy pierwotne w podziale na I i II nie zgrywają się z odp

silnia: dobra, z peirwszego rpzedziału wychodzi x∊<−3,−2), a z drugiego <−2, +∞), co w połączeniu z x≠−1 daje mi x∊<−3,−1) (−1, +∞)

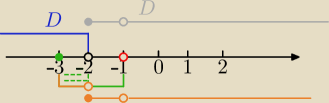
Mila: I) x∊(−∞,−2) (x+3)*(x+1)≤0⇔ x∊<−3,−1) i x∊(−∞,−2) patrz na ilustrację na osi liczbowej x∊<−3,−2) lub II) możesz tak: x∊<−2, +∞)\{−1}

2(x+1)
	≥1
x+1

2≥1 −prawda dla x∊<−2,∞)\{−1} odp. x∊<−3,−1)∪(−1,∞) suma przedziałów albo taki zapis: x∊<−3,∞)\{−1} przedział z wyłączeniem liczby (−1)